National 5MathsSQARevision NotesTrigonometric SkillsTrigonometry with TrianglesProblem-Solving with Triangles

Problem-Solving with Triangles (SQA National 5 Maths): Revision Note

Exam code: X847 75

Roger B

Written by: Roger B

Reviewed by: Dan Finlay

Updated on

Problem-solving with triangles

How do I decide which non-right-angled trigonometry rule to use?

  • A question will usually not tell you which rule to use

  • Different rules are required depending on the situation

    • You need to be able to decide which is appropriate to use

    • Think about what information you have and what you want to find

  • This table summarises the possibilities:

If you know

And you want to know

Use

Two sides and an angle opposite one of the sides

The angle opposite the other side

Sine rule

Two angles and a side opposite one of the angles

The side opposite the other angle

Sine rule

Two sides and the angle between them

The third side

Cosine rule

All three sides

Any angle

Cosine rule

Two sides and the angle between them

The area of the triangle

Area of a triangle rule

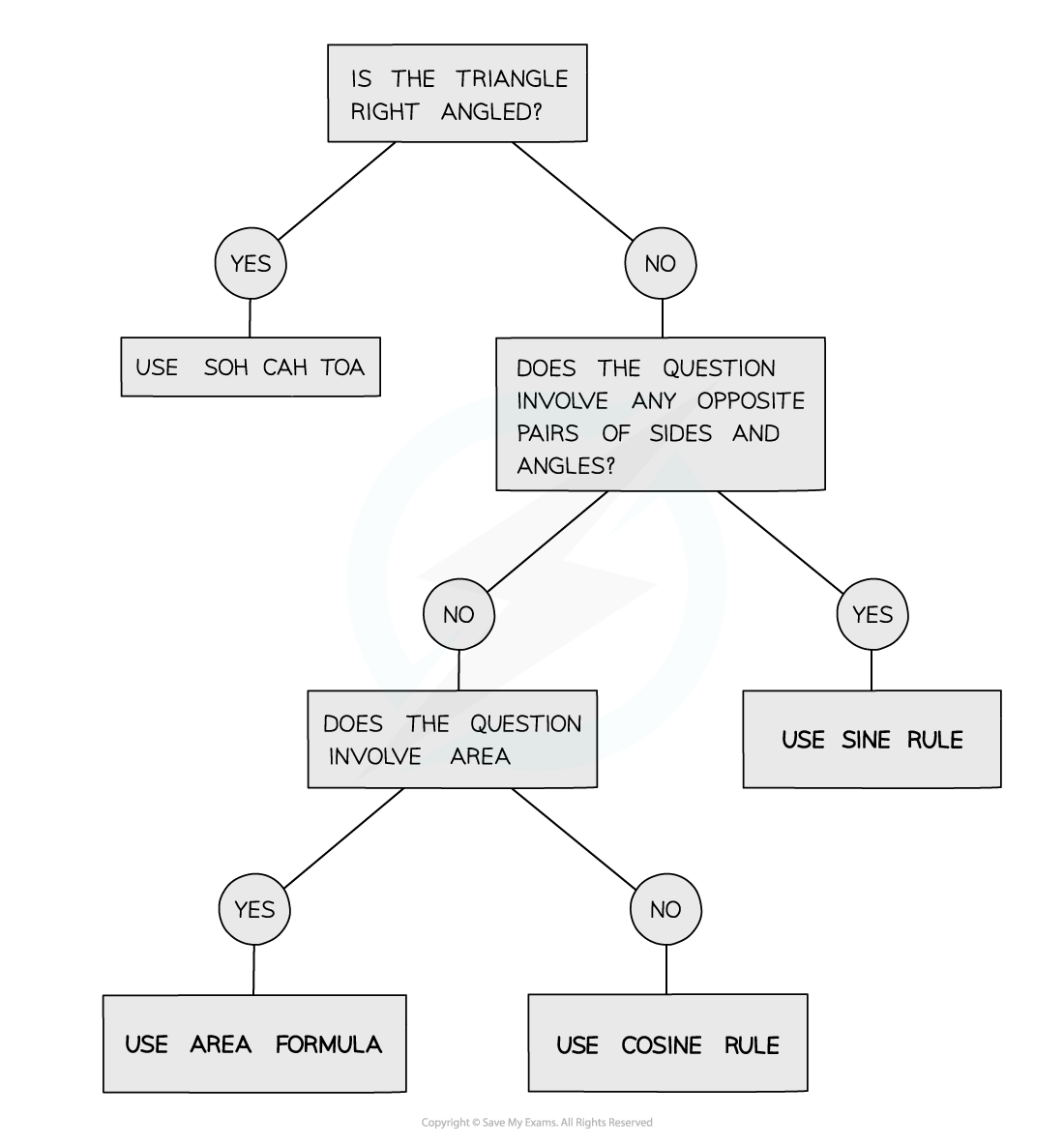
Flow chart to determine which rule or formula to use.

Will I need to use multiple trigonometry rules in the same question?

  • Harder questions will require you to use more than one trig rule

    • For example, you may need the sine rule followed by the cosine rule

  • The area formula only works for an angle between two sides

    • If you are not given this setup, you may need to use the sine or cosine rule first

  • If it looks like no rule would work, remember that all angles in a triangle sum to 180°

    • This often helps to find a missing angle

  • Also be sure you know your right-angled trigonometry rules from your National 4 Maths course:

    • Pythagoras' theorem

    • SOHCAHTOA (i.e. trigonometric ratios for sin, cos and tan)

Examiner Tips and Tricks

By drawing an appropriate line on a question diagram, you can add a right angle that was not originally indicated. This can allow you to use right-angled trigonometry rules, and may be the key to answering a question.

Worked Example

Catie and Avery are watching the launch of a model rocket.

In the diagram below, C and A represent the positions of Catie and Avery, and R represents the position of the rocket at the highest point in its flight.

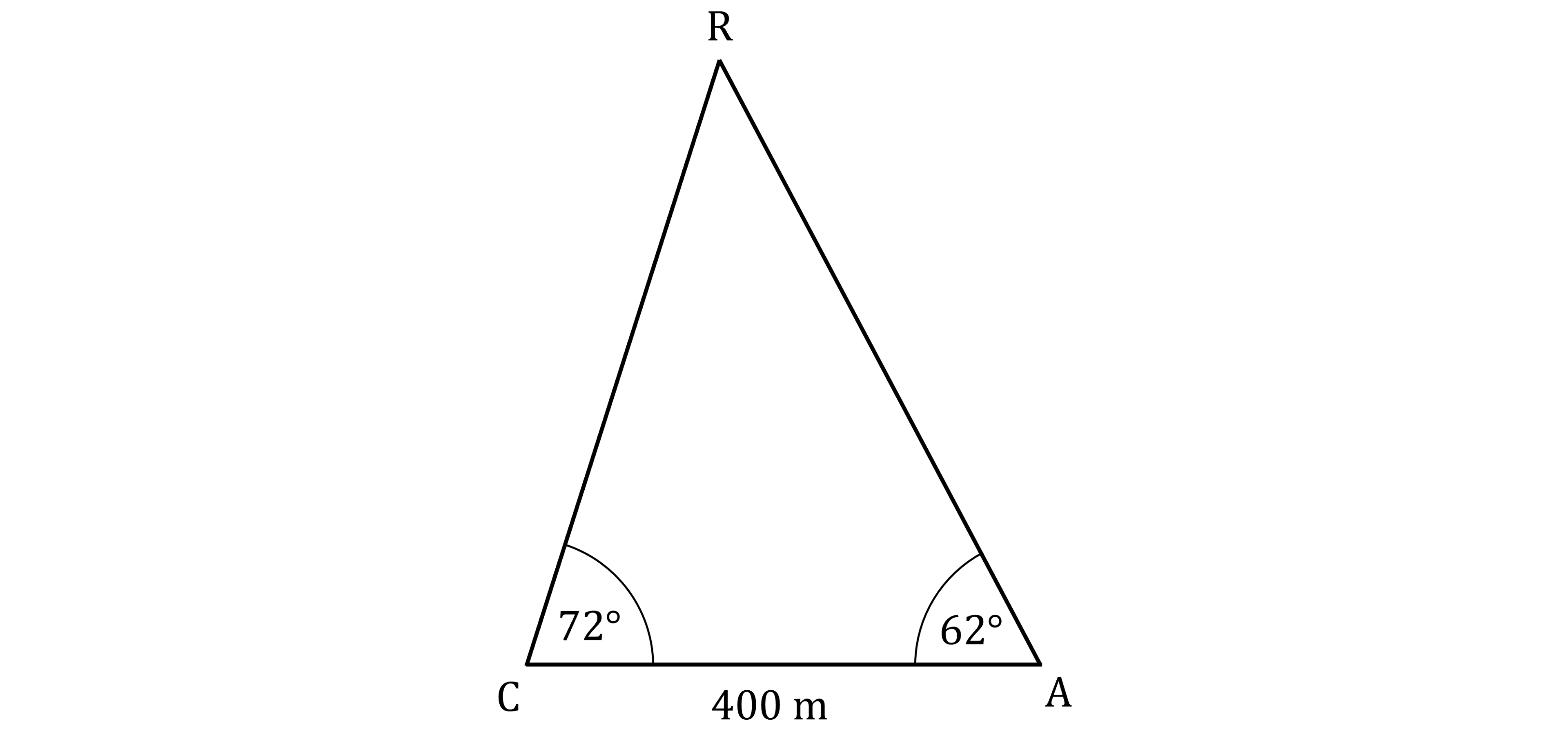
Triangle with vertices R, A, C. Angle at C is 72 degrees, angle at A is 62 degrees. Side AC is 400 m.

  • The angle of elevation of the rocket from Catie is 72°

  • The angle of elevation of the rocket from Avery is 62°

  • Catie and Avery are 400 metres apart on level ground

Calculate the height of the rocket above the ground at the highest point in its flight.

Answer:

Initially looking at the diagram in the question, it looks like

  • there aren't any right angles, so you can't use right-angled trigonometry

  • there aren't any angles opposite sides, so you can't use the Sine Rule

  • there is no angle between two sides so you can't use the Cosine Rule

This is a job for some creative problem solving!

First use 180° in a triangle to find the missing angle

180 - 72 - 62 = 46°

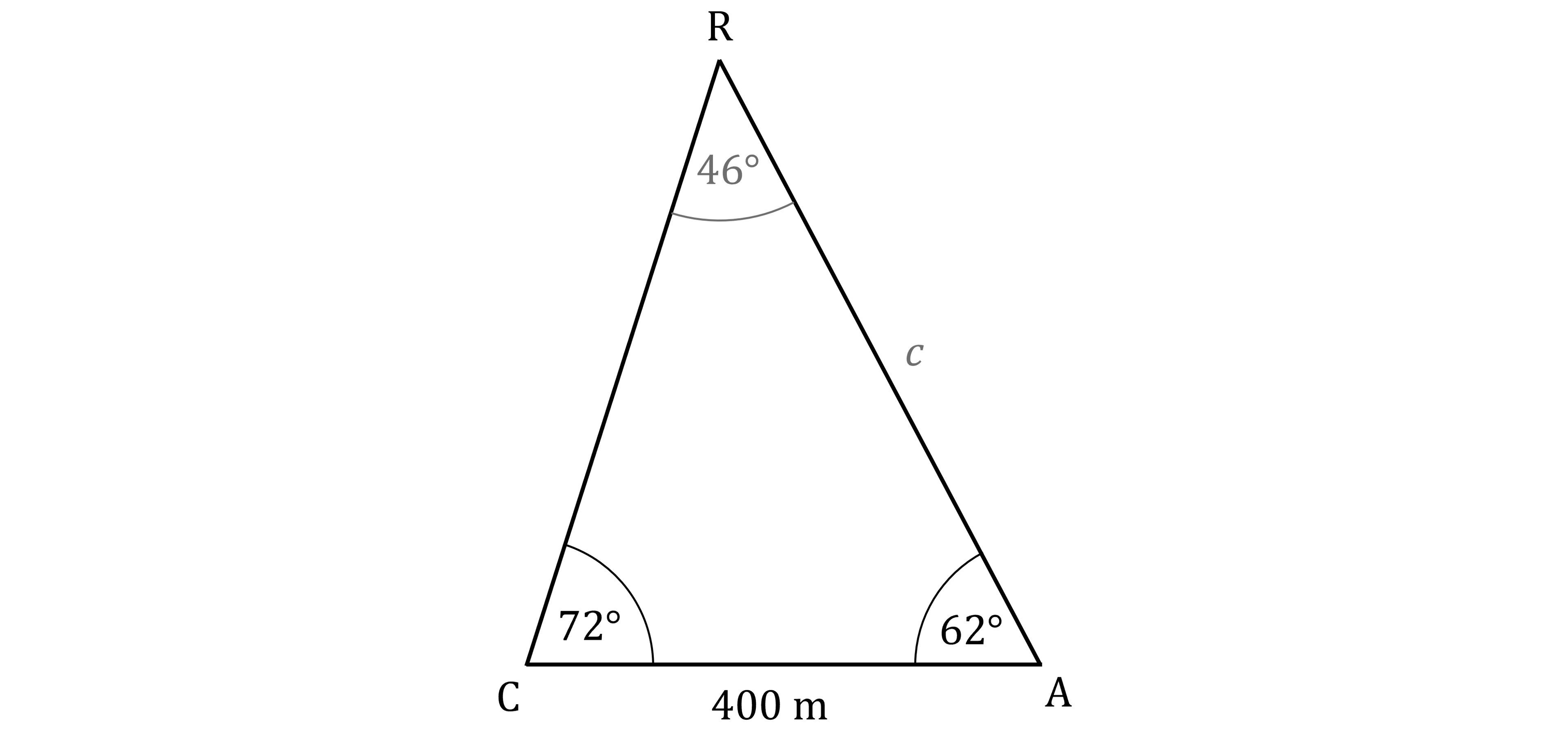
Triangle with vertices labelled R, C and A. Angle at R is 46°, angle at C is 72°, angle at A is 62°. Side CA measures 400 m, and side RC is labelled c.

Now you have a side opposite an angle, so you can use the Sine Rule to find the length of side AR (marked c in the diagram)

  • You could also use the Sine Rule to find side CR, which would lead you to the same final answer

table row cell fraction numerator c over denominator sin 72 end fraction end cell equals cell fraction numerator 400 over denominator sin 46 end fraction end cell row c equals cell fraction numerator 400 over denominator sin 46 end fraction cross times sin 72 end cell row c equals cell 528.849656... end cell end table

Now you can draw a vertical line down to the ground from point R

  • This will make a right angle with CA

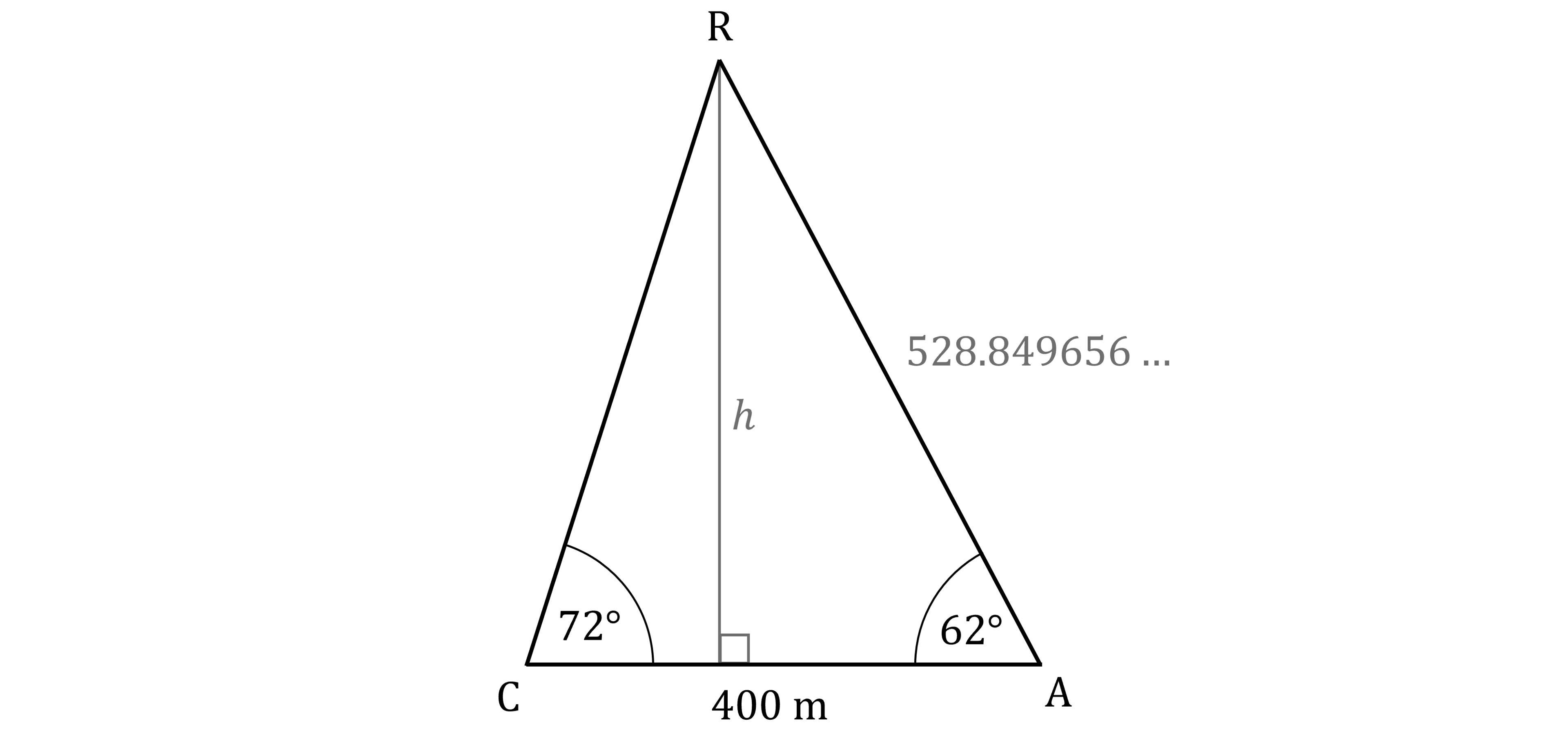
Diagram of triangle CRA, with horizontal base CA. Angle at C is 72°and angle at A is 62°. Side AC is 400m and side AR is labelled 528.849656... . Perpendicular height h from R has been drawn from R to base AC.

With that right angle, you can use the sine ratio from SOHCAHTOA to find the height h

sin 62 equals fraction numerator h over denominator 528.849656... end fraction

table row h equals cell 528.849656... cross times sin 62 end cell row blank equals cell 466.946531... end cell end table

Round to a sensible degree of accuracy

  • Unless a question tells you otherwise, 3 significant figures is usually a good choice

467 m  (3 s.f.)

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Previous:BearingsNext:Mean & Standard Deviation
    Author
    Reviewer
    Roger B

    Author: Roger B

    Expertise: Maths Content Creator

    Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.

    Dan Finlay

    Reviewer: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.