GCSEMathsWJECMaths & Numeracy (Double Award)HigherRevision NotesAlgebraCoordinate Geometry & Linear GraphsCoordinates on Parallelograms

Coordinates on Parallelograms (WJEC GCSE Maths & Numeracy (Double Award)): Revision Note

Exam code: 3320

Jamie Wood

Written by: Jamie Wood

Reviewed by: Mark Curtis

Updated on

Coordinates on Parallelograms

What are the properties of a parallelogram?

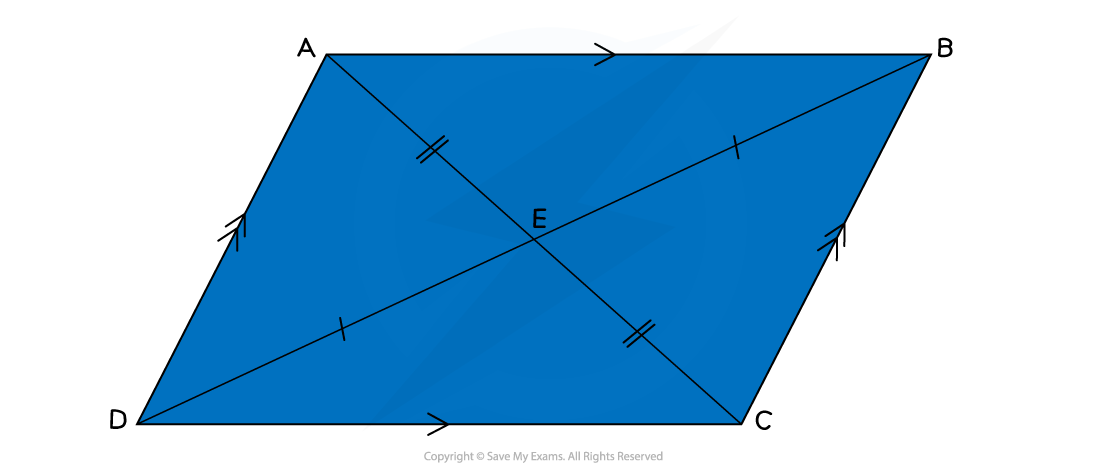
  • A parallelogram is a special quadrilateral (it has 4 sides)

    • with two pairs of parallel sides

    • where the sides in each pair are equal in length

      • This does not mean all sides must be equal

  • The diagonals of a parallelogram bisect each other

    • This means they cut each other exactly in half

      • This does not mean they always cut at right-angles

  • A rhombus is a special case of a parallelogram, where

    • all 4 sides are the same length

    • the diagonals cut each other at right angles

A blue parallelogram ABCD with diagonal lines intersecting at point E, showing equal segment marks on lines indicating symmetry.

How do I find the coordinates of a missing vertex on a parallelogram?

  • To find the coordinates of a missing vertex, either:

    • count the squares

      • e.g. A to B is x units across and y units up

      • so D to C must also be x units across and y units up

    • or force the midpoints of the diagonals to be the same point

      • The midpoints of diagonal AC is equal to the midpoint of diagonal BD

      • The midpoint of open parentheses x subscript 1 comma space y subscript 1 close parentheses and open parentheses x subscript 2 comma space y subscript 2 close parentheses is open parentheses fraction numerator x subscript 1 plus x subscript 2 over denominator 2 end fraction space comma fraction numerator y subscript 1 plus y subscript 2 space over denominator 2 end fraction close parentheses

Worked Example

The vertices A (1, 4), B (5, 6) and C (11, 2) form three corners of the parallelogram ABCD.

Find the coordinates of the fourth vertex, D.

Answer:

If the parallelogram is ABCD, this is the order of the vertices

This means the parallel sides are AC and BD

Make a sketch to help you; it can help to label D as open parentheses x comma space y close parentheses

Use the given coordinates to place the points in approximately the correct positions relative to each other

Diagram of parallelogram ABCD with vertices A(1,4), B(5,6), C(11,2), and D(x,y). Arrows indicate parallel sides AB and DC

Method 1 (counting squares)

Using the sketch above, you can see that BC is parallel to AD

Find how to get from B (5, 6) to C (11, 2) by considering the difference in the x coordinates (horizontal), and the difference in the y coordinates (vertical)

B to C = +6 units horizontally, -4 units vertically

AD must be the same, as it is parallel to BC

A is (1, 4)

Apply "+6 units horizontally, -4 units vertically" to A (1, 4) to find D

D is (1+6, 4-4)

D is (7, 0)

Method 2 (midpoints of diagonals are equal)

As the diagonals of a parallelogram bisect each other, the midpoint of both diagonals will be in the same place

Find the midpoint of the known diagonal AC using open parentheses fraction numerator x subscript 1 plus x subscript 2 over denominator 2 end fraction space comma fraction numerator y subscript 1 plus y subscript 2 space over denominator 2 end fraction close parentheses

open parentheses fraction numerator 1 plus 11 over denominator 2 end fraction space comma fraction numerator 4 plus 2 space over denominator 2 end fraction close parentheses equals open parentheses 6 comma space 3 close parentheses

The midpoint of BD must be the same

open parentheses fraction numerator 5 plus x over denominator 2 end fraction space comma space fraction numerator 6 plus y over denominator 2 end fraction close parentheses equals open parentheses 6 comma space 3 close parentheses

This gives you two equations to solve

fraction numerator 5 plus x over denominator 2 end fraction equals 6 and fraction numerator 6 plus y over denominator 2 end fraction equals 3

Solve the first equation

table row cell fraction numerator 5 plus x over denominator 2 end fraction end cell equals 6 row cell 5 plus x end cell equals 12 row x equals 7 end table

Solve the second equation

table row cell fraction numerator 6 plus y over denominator 2 end fraction end cell equals 3 row cell 6 plus y end cell equals 6 row y equals 0 end table

You now know the coordinates of D open parentheses x comma space y close parentheses

D is (7, 0)

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Previous:Midpoint of a LineNext:Coordinates using Distance & Angle
    Author
    Reviewer
    Jamie Wood

    Author: Jamie Wood

    Expertise: Maths Content Creator

    Jamie graduated in 2014 from the University of Bristol with a degree in Electronic and Communications Engineering. He has worked as a teacher for 8 years, in secondary schools and in further education; teaching GCSE and A Level. He is passionate about helping students fulfil their potential through easy-to-use resources and high-quality questions and solutions.

    Mark Curtis

    Reviewer: Mark Curtis

    Expertise: Maths Content Creator

    Mark graduated twice from the University of Oxford: once in 2009 with a First in Mathematics, then again in 2013 with a PhD (DPhil) in Mathematics. He has had nine successful years as a secondary school teacher, specialising in A-Level Further Maths and running extension classes for Oxbridge Maths applicants. Alongside his teaching, he has written five internal textbooks, introduced new spiralling school curriculums and trained other Maths teachers through outreach programmes.