2D Representations of 3D Shapes (WJEC GCSE Maths & Numeracy (Double Award)): Revision Note
Exam code: 3320
2D Representations of 3D Shapes
How can 3D shapes be represented in 2D?
Previous notes in this topic have already covered some of the ways 3D shapes can be represented in 2D (i.e. on paper)
Nets of 3D shapes
A net of a solid is a 2D drawing that can be cut out and folded to make a 3D shape
Plans and elevations
They are two-dimensional views of a three-dimensional object
They are the mathematical shapes you would see when looking directly at a 3D object from a given direction (the front, the side, or the top)
Another method is to use isometric drawings
Examiner Tips and Tricks
In the exam, you will not be expected to draw 2D representations of 3D shapes. The focus of the question will be on interpreting the drawing.
E.g. Finding the volume of a cuboid from a given drawing of its net.
What is an isometric drawing?
An isometric drawing is a way to draw 3D shapes in 2D more accurately
They are often used in technical documents, e.g. in instruction manuals or by architects
An isometric drawing does not have a "vanishing point" like a perspective drawing
This means lines which are meant to be parallel in 3D, will also be parallel in 2D
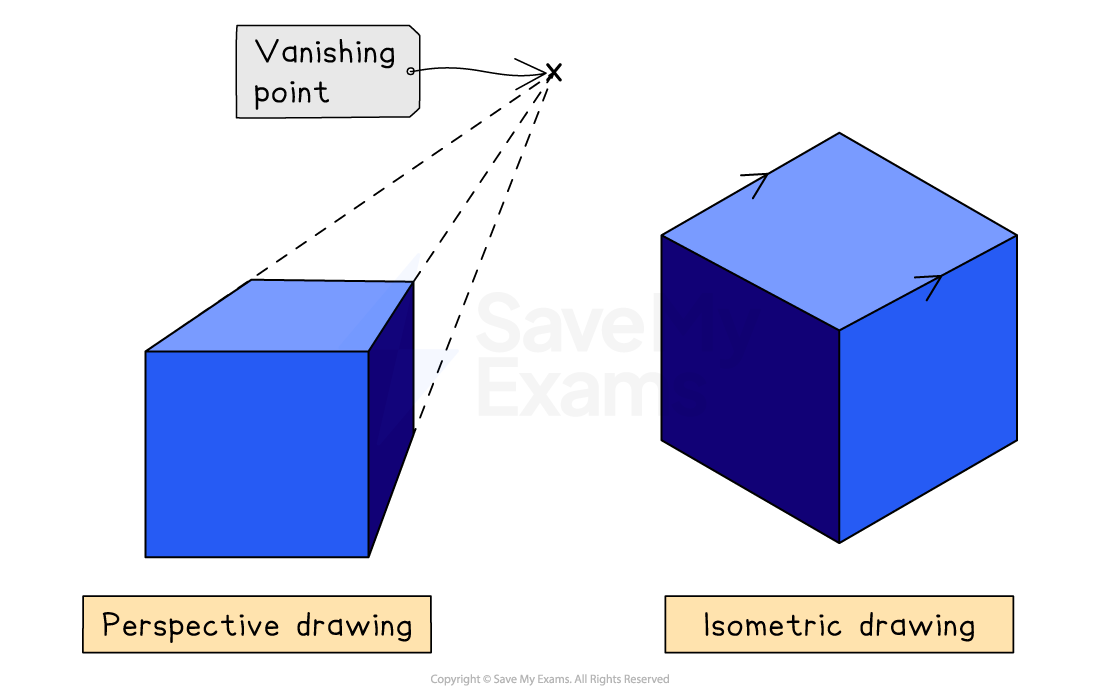
Isometric drawings have one edge of the shape "closest" to the viewer
They can be drawn using special isometric paper which has dots or lines at the correct angle to one another
Worked Example
An object made from cubes which each have volume 1 cm3 has been drawn on isometric paper and is shown below.
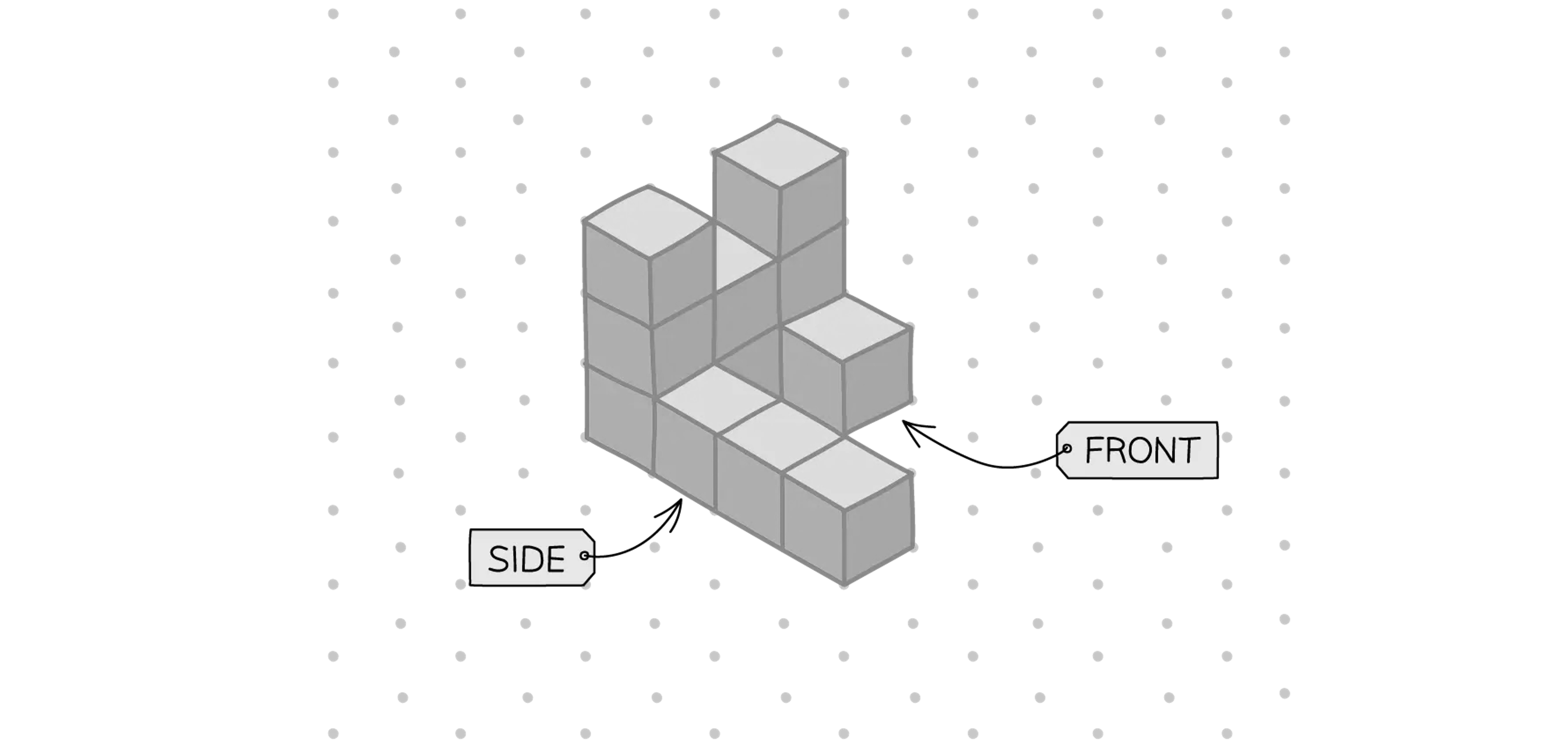
(a) Calculate the surface area of the front elevation of the object.
Answer:
It can be helpful to colour each of the three views in three different colours
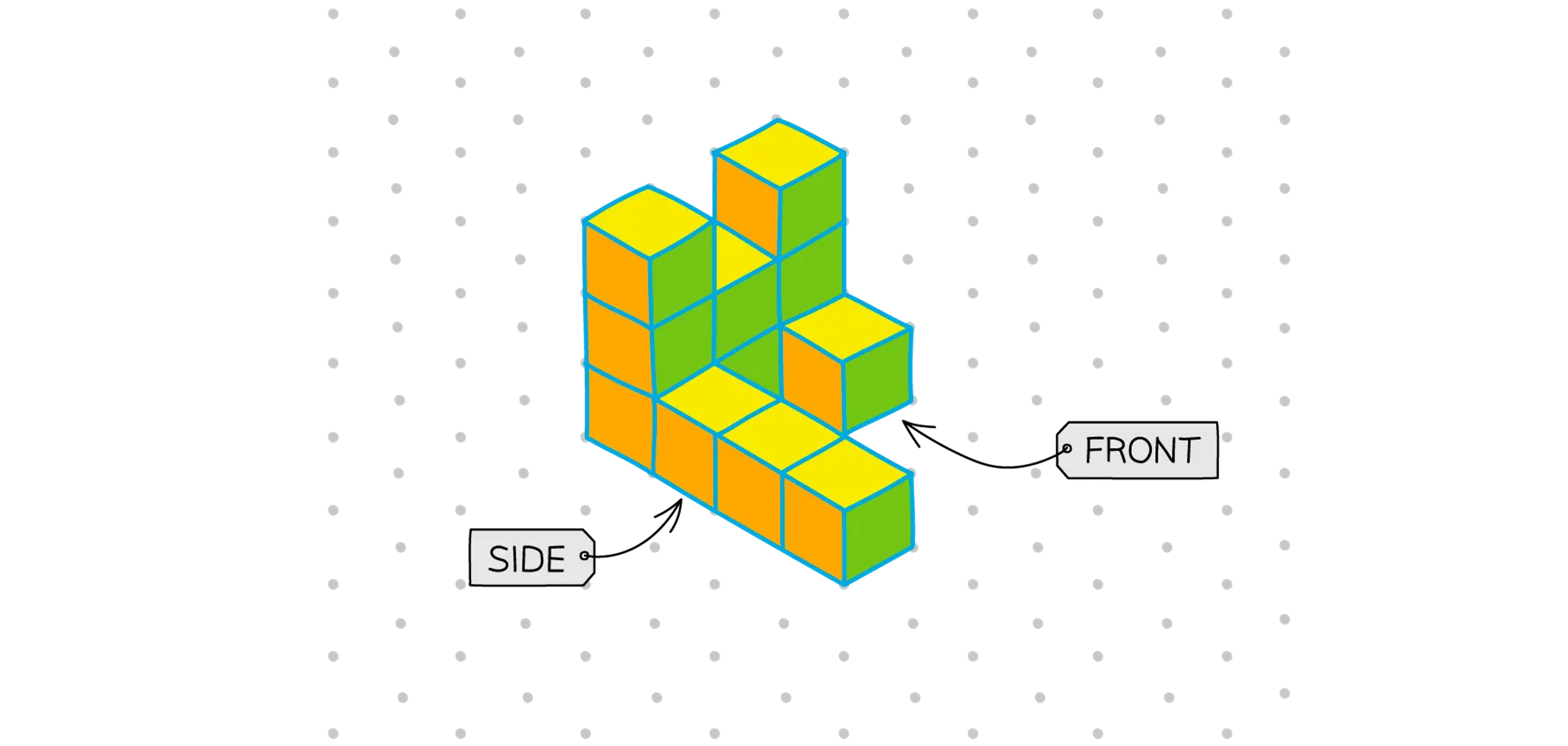
Using the drawing, you can see there are 8 square faces which can be seen in the front view
As each cube has a volume of 1 cm3, the edges of the cube must all be 1 cm
This means the area of each face of each cube is 1 cm2
Multiply this by 8
8 cm2
(b) What assumption have you made in your answer to part (a)?
Answer:
An isometric drawing is still only one perspective of the object, there may be "hidden" cubes which cannot be seen from the view you are given
E.g. in the diagram above there could be a cube hidden "underneath" the object, so that the front view looks as below
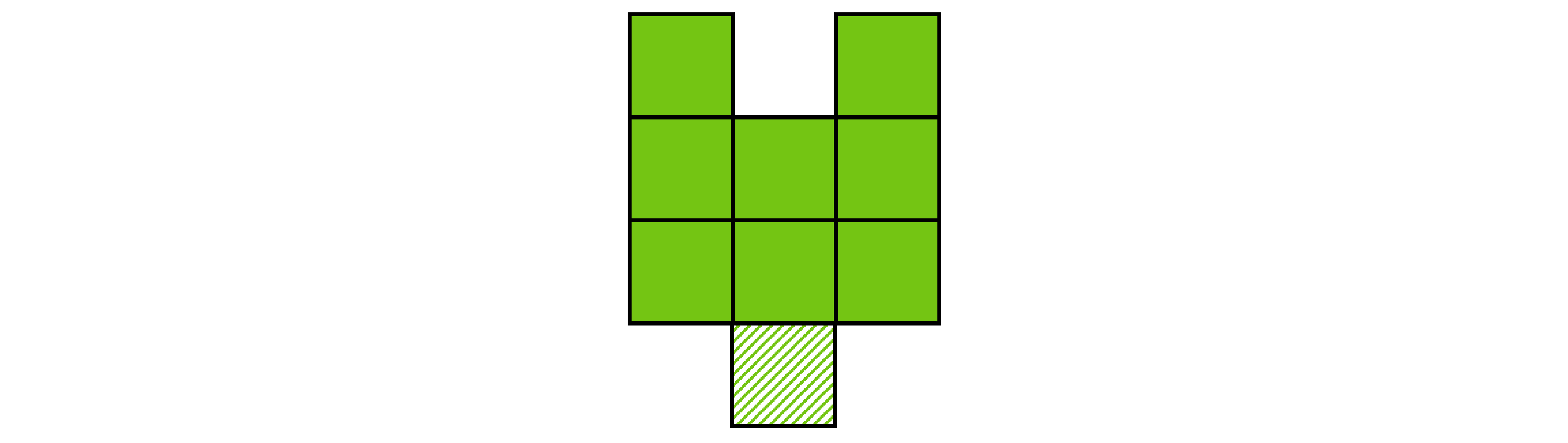
Assumed that there are no cubes which cannot be seen in the diagram

Unlock more, it's free!
Did this page help you?