GCSEMathsWJECMaths & Numeracy (Double Award)HigherRevision NotesNumberInformation in Tables, Charts & DiagramsVenn Diagrams

Venn Diagrams (WJEC GCSE Maths & Numeracy (Double Award)): Revision Note

Exam code: 3320

Jamie Wood

Written by: Jamie Wood

Reviewed by: Mark Curtis

Updated on

Venn diagrams

What is a Venn diagram?

  • A Venn diagram is a way to illustrate events from an experiment and are particularly useful when there is an overlap (or lack of) between possible outcomes

  • A Venn diagram consists of

    • a rectangle representing the sample space

    • a circle for each event

    • Circles may or may not overlap depending on which outcomes are shared between events

    • Circles may be separate (no overlap) if no outcomes are shared

    • One circle may be entirely within another if all outcomes are shared

How do I interpret a Venn diagram?

  • The outer rectangle represents the sample space (all possible outcomes from the experiment)

    • It is often referred to as the universal set

    • It may be labelled with any of epsilon comma space S comma space U comma space xi or calligraphic E depending on the source

  • Circles are labelled with their event name (A, B, etc)

  • The numbers inside a Venn diagram will represent either a frequency or a probability

    • In the case of probabilities being shown, all values should total 1

  • Read the revision note Probability from Venn Diagrams in the Probability section for more detail about finding probabilities from Venn diagrams

Two Venn diagrams compare frequencies and probabilities for events A and B. The left shows counts, the right shows matching probabilities.

Examiner Tips and Tricks

Remember to draw the box around a Venn diagram. It represents all possible outcomes of the experiment, so is a crucial part of the diagram!

Examiner Tips and Tricks

When completing a Venn diagram, check that the frequencies sum to the correct total (or that the probabilities sum to 1).

Worked Example

At a school activities fair, 60 students signed up for three options: Coding (C), Robotics (R), and Photography (P).

Coding and Robotics both take place on the main campus, and some students do both.

Photography sessions are held at a partner art college across town, so no student can join Photography and either of the other two clubs.

The following information was collected:

  • 26 students signed up for Coding

  • 22 students signed up for Robotics

  • 12 students signed up for Photography

  • 8 students signed up for Coding and Robotics

  • There are 60 students in total

(a) Complete the Venn diagram below to show the number of students in each region.

Three circles in a rectangle labelled epsilon, with the left two overlapping slightly.

Answer:

You are told that no one can do Photography and one of the other two activities

The separate circle must therefore be Photography (P), and you know that 12 signed up for Photography

Left circle is C, overlapping circle is R. Separate circle is P. 12 is in the P circle

Start with the overlapping region

You are told that 8 students signed up for Coding and Robotics

8 in the overlap between C and R

You are told that 26 signed up for coding in total

26 - 8 = 18

You are told that 22 signed up for Robotics in total

22 - 8 = 14

18 in C only, 14 in R only

Find how many students did not sign up to any of the three clubs (there were 60 in total)

60 - 18 - 8 - 14 - 12 = 8

Fill this in inside the rectangle, but outside any circle to complete the Venn diagram

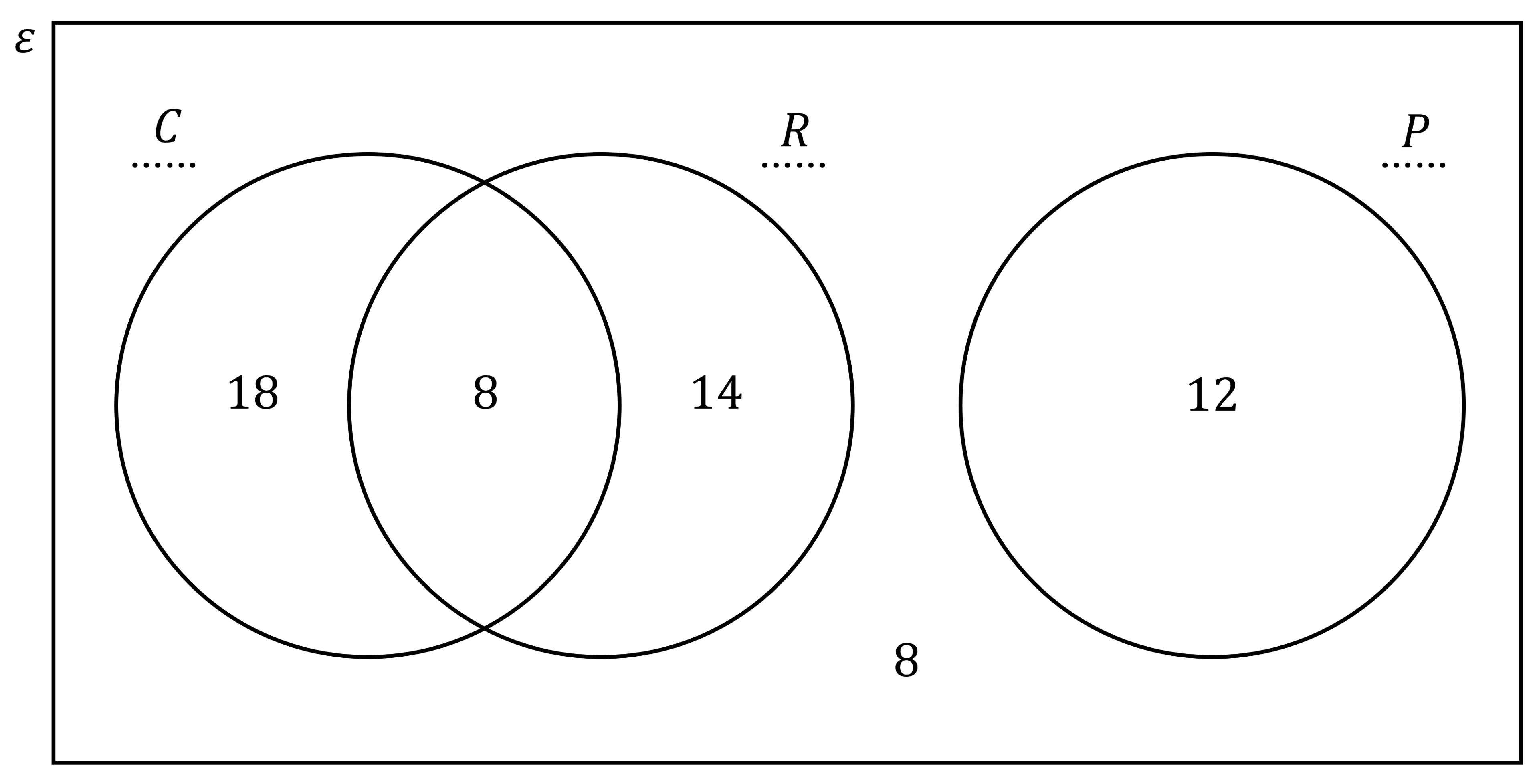
8 in the rectangle but not in any circle

(b) Find how many students sign up to:

(i) more than 1 of the clubs,

(ii) coding but not robotics

(iii) only 1 club.

Answer:

(i)

More than 1 of the clubs is the overlapping region between C and R

8 students sign up to more than 1 club

(ii)

Coding but not robotics is the "C only" region

18 students sign up to Coding but not Robotics

(iii)

Only 1 club is the "C only" region plus the "R only" region plus the "P only" region

18 + 14 + 12 = 44

44 students sign up to only 1 club

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Previous:Information in Tables, Charts & DiagramsNext:Money Calculations
    Author
    Reviewer
    Jamie Wood

    Author: Jamie Wood

    Expertise: Maths Content Creator

    Jamie graduated in 2014 from the University of Bristol with a degree in Electronic and Communications Engineering. He has worked as a teacher for 8 years, in secondary schools and in further education; teaching GCSE and A Level. He is passionate about helping students fulfil their potential through easy-to-use resources and high-quality questions and solutions.

    Mark Curtis

    Reviewer: Mark Curtis

    Expertise: Maths Content Creator

    Mark graduated twice from the University of Oxford: once in 2009 with a First in Mathematics, then again in 2013 with a PhD (DPhil) in Mathematics. He has had nine successful years as a secondary school teacher, specialising in A-Level Further Maths and running extension classes for Oxbridge Maths applicants. Alongside his teaching, he has written five internal textbooks, introduced new spiralling school curriculums and trained other Maths teachers through outreach programmes.