IBPhysicsDPSLRevision NotesNuclear & Quantum PhysicsFusion & StarsEnergy Released in Fusion Reactions

Energy Released in Fusion Reactions (DP IB Physics): Revision Note

Katie M

Author

Katie M

Last updated

DP Physics: SLDP Physics: HL

Energy Released in Fusion Reactions

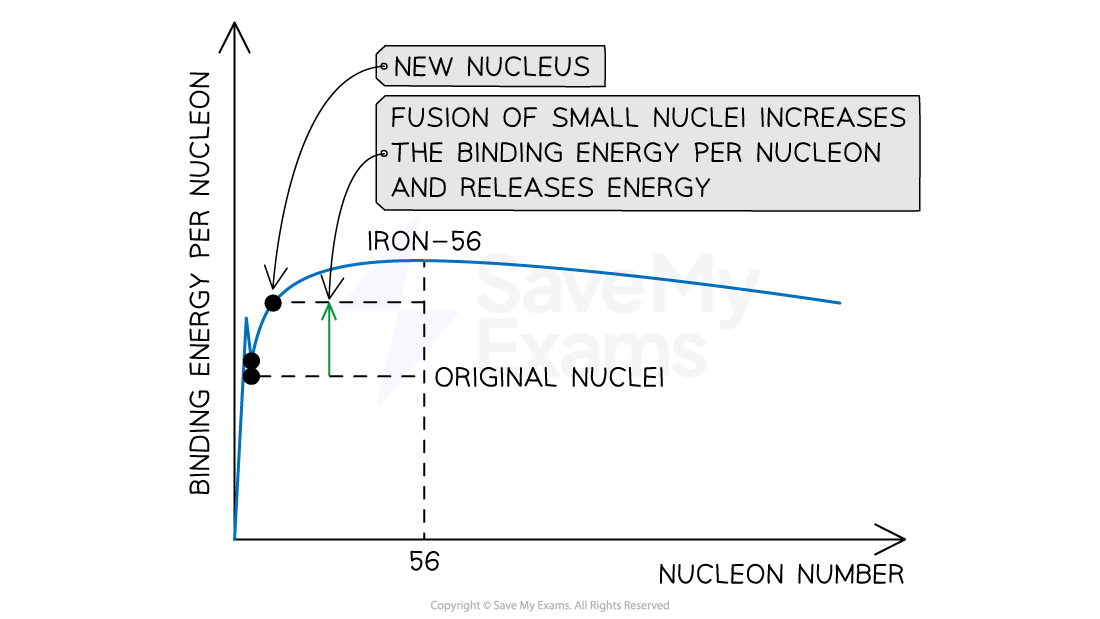
  • When two small nuclei undergo fusion, the larger nucleus produced as a result will have a higher binding energy per nucleon than the original two nuclei

    • There is a mass defect between the original nuclei and the new nucleus

    • Energy is released as a result of the difference in binding energy

  • For example, when two deuterium nuclei open parentheses straight H presubscript 1 presuperscript 2 close parentheses fuse into one helium nucleus open parentheses He presubscript 2 presuperscript 4 close parentheses

    • the binding energy of a helium nucleus is about 28 MeV

    • the total binding energy of the deuterium nuclei is about 4 MeV

    • the energy released is 28 - 4 = 24 MeV

Graph showing binding energy per nucleon against nucleon number, highlighting that the fusion of small nuclei increases the binding energy per nucleon of the new nucleus compared to the original nuclei.
The energy released from fusion reactions is due to the mass defect between original nucleis and new nucleus which is produced from them

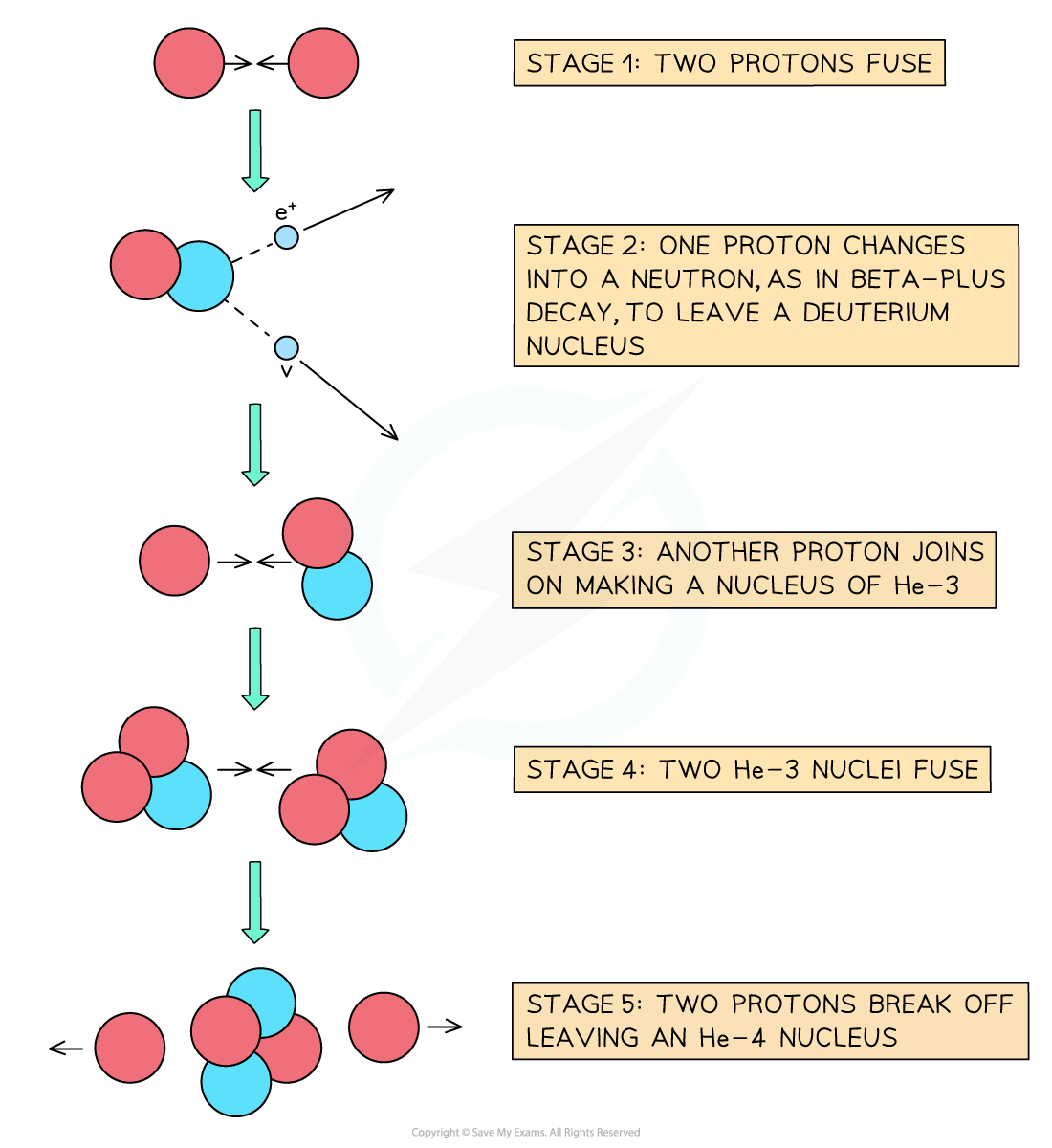
  • In the hot core of a star, fusion begins with two protons combining to form a deuterium nucleus

  • The deuterium nuclei go on to form a helium nucleus, plus the release of energy

    • This provides fuel for the star to continue burning

The proton-proton chain

The proton-proton fusion process in five stages Stage 1: Two protons fuse Stage 2: One proton changes into a neutron, as in beta-plus decay, to leave a deuterium nucleus Stage 3: Another proton joins on, making a nucleus of helium-3 Stage 4: Two helium-3 nuclei fuse Stage 5: Two protons break off, leaving a helium-4 nucleus
The proton-proton chain involves a series of nuclear reactions which produces a helium nucleus from the fusion of four protons

Worked Example

In the Sun, fusion occurs via a process known as the proton-proton chain.

It is predicted that 80% of the total power output of the Sun is produced through the following cycle:

open table row cell straight H presubscript 1 presuperscript 1 space plus space straight H presubscript 1 presuperscript 1 space rightwards arrow space straight H presubscript 1 presuperscript 2 space plus space straight e presubscript 1 presuperscript 0 superscript plus space plus space nu subscript straight e end cell row cell straight H presubscript 1 presuperscript 1 space plus space straight H presubscript 1 presuperscript 2 space rightwards arrow space He presubscript 2 presuperscript 3 space plus space straight gamma end cell row cell He presubscript 2 presuperscript 3 space plus space He presubscript 2 presuperscript 3 space rightwards arrow space He presubscript 2 presuperscript 4 space plus space straight H presubscript 1 presuperscript 1 space plus space straight H presubscript 1 presuperscript 1 end cell end table space close curly brackets space space 4 straight H presubscript 1 presuperscript 1 space rightwards arrow space He presubscript 2 presuperscript 4 space plus space 2 straight e presubscript 1 presuperscript 0 superscript plus space plus space 2 nu subscript straight e (overall reaction)

nucleus

rest mass / u

hydrogen-1

1.007825

helium-4

4.002603

The neutrinos produced in the first step carry away 2% of the energy released by the process.

Determine the mass of hydrogen-1 that must be fused each second to produce this output.

Luminosity of the Sun = 3.85 × 1026 W.

Answer:

Step 1: Determine the energy released per overall fusion reaction

  • In the overall reaction, 4 hydrogen-1 nuclei fuse into a helium-4 nucleus, so the mass defect is:

increment m = 4(1.007825u) − 4.002603u

increment m = 0.028697u

  • Where atomic mass unit, u = 1.66 × 10−27 kg

  • Using mass-energy equivalence, the energy released by one reaction is:

increment E space equals space increment m c squared

increment E = 0.028697 × (1.66 × 10−27) × (3 × 108)2

increment E = 4.287 × 10−12 J

Step 2: Determine the energy released minus the energy that is carried away by neutrinos

  • Per reaction, neutrinos carry away 2% of 4.287 × 10−12 J, so 98% of the energy contributes to the luminosity of the Sun

increment E = 0.98 × (4.287 × 10−12) = 4.201 × 10−12 J

Step 3: Determine the number of fusion reactions that happen each second

  • This process accounts for 80% of the luminosity of the Sun,

  • So, the total power output of the reaction = 0.8 × (3.85 × 1026) W

  • The number of fusion reactions each second is:

number of reactions = fraction numerator power space output over denominator energy space released space per space reaction end fraction

number of reactions = fraction numerator 0.8 cross times open parentheses 3.85 cross times 10 to the power of 26 close parentheses over denominator 4.201 cross times 10 to the power of negative 12 end exponent end fraction = 7.332 × 1037 s−1

Step 4: Determine the mass of hydrogen that fuses each second

  • Every reaction fuses 4 hydrogen-1 nuclei, so the mass per reaction is 4 × 1.007825u

  • The mass of hydrogen-1 that fuses each second in this process is

mass of hydrogen-1 = 4u × number of reactions

mass of hydrogen-1 = 4 × 1.007825 × (1.66 × 10−27) × (7.332 × 1037)

mass of hydrogen-1 = 4.91 × 1011 kg s−1

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcards
    Previous:Fusion Reactions in StarsNext:Star Formation
    Katie M

    Author: Katie M

    Expertise: Physics Content Creator

    Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.