A LevelPhysicsAQARevision NotesAstrophysicsCosmologyHubble's Law

Hubble's Law (AQA A Level Physics) : Revision Note

Katie M

Author

Katie M

Last updated

Hubble's Law

  • Analysis of the light from distant galaxies reveals a clear relationship between the distance of the galaxy from Earth and the amount of red shift

  • This relationship is known as Hubble’s law, which states:

The recessional velocity of a galaxy is proportional to its distance from Earth

  • This can be expressed mathematically as:

v space equals space H d

  • Where:

    • v = recessional velocity of an object (km s−1)

    • H = Hubble constant (km s−1 Mpc−1)

    • d = distance between the object and the Earth (Mpc)

  • In terms of red shift z, this can also be written as

v space equals space z c space equals space H d

z space equals space fraction numerator H d over denominator c end fraction

  • Where:

  • Hubble’s law shows that:

    • the further away a galaxy is from the Earth, the greater the red shift, and the faster it is moving away

    • the closer a galaxy is to the Earth, the smaller the red shift, and the slower it is moving away

Graph of Hubble's Law

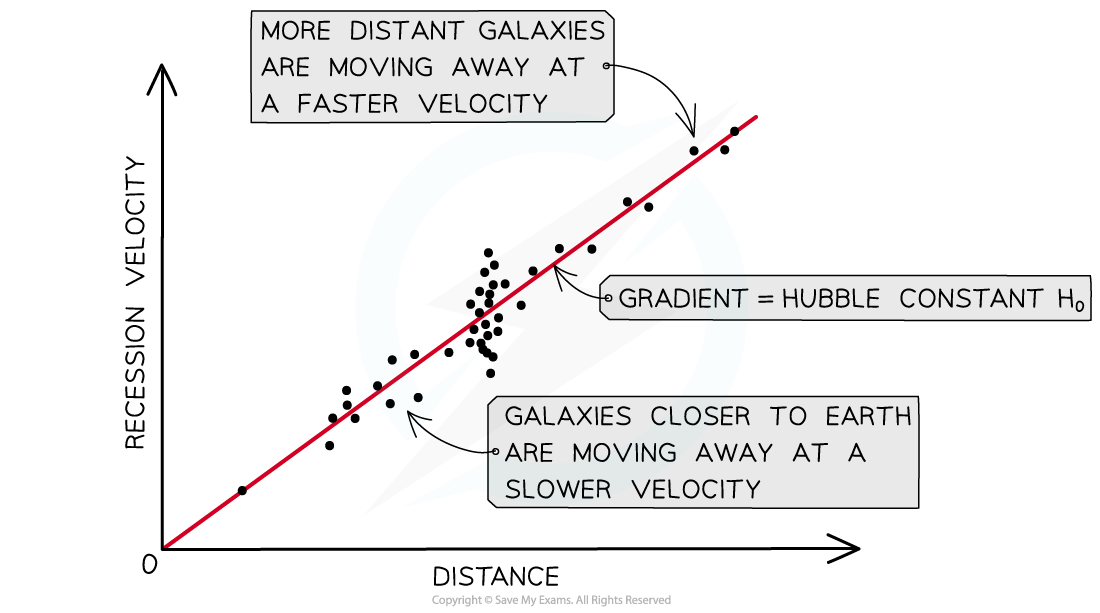
Hubbles Law Graph, downloadable AS & A Level Physics revision notes

A key aspect of Hubble’s law is that the furthest galaxies appear to move away the fastest

The Hubble Constant

  • The constant of proportionality H in Hubble’s law is known as the Hubble constant:

H space equals space v over d

  • The value for the Hubble constant has been estimated using data from thousands of galaxies and other sources, such as standard candles

  • A value for the Hubble constant can be determined by

    • measuring values of red shift z and distance for a range of galaxies

    • plotting a graph of velocity open parentheses v space equals space z c close parentheses against distance d

    • calculating the gradient (equal to H) for the plotted points

  • Our current best estimate of the Hubble constant, based on CMB observations by the Planck satellite, is:

H = 67.4 ± 0.5 km s−1 Mpc−1

  • Note: this value is constantly under review as more data is collected

Worked Example

The graph shows how the recessional velocity v of a group of galaxies varies with their distance d from the Earth.

5-12-5-we-q_ocr-al-physics

Use the graph to determine a value for the Hubble constant and state its unit.

Answer:

Step 1: Recall Hubble's Law and the Hubble constant

  • Hubble’s Law: v space equals space H d

  • The gradient of the speed-distance graph = H

Step 2: Read values of v and d from the graph

5-12-5-we-solution_ocr-al-physics

  • From the graph: v = 20 000 km s–1

  • From the graph: d = 305 MPc

Step 3: Calculate the gradient of the graph

H space equals space fraction numerator 20 space 000 space minus space 0 over denominator 305 space minus space 0 end fraction space equals space 65.6 space km space straight s to the power of negative 1 end exponent space Mpc to the power of negative 1 end exponent

Hubble constant:  H = 66 km s–1 Mpc–1

Worked Example

Measurements of type 1a supernovae are used to find a value for the Hubble constant. The distance from Earth is known for many type 1a supernovae.

Describe how these values of distance are used, with other data, to find the Hubble constant.

Your answer should include:

  • the other data needed and how these data are used

  • the graph plotted, including appropriate units for the axes

  • how the Hubble constant is obtained and any limitations on the result.

Answer:

Step 1: Describe the data needed for the determination of the Hubble constant and how it will be used

  • The Hubble constant can be described by the ratio of recession velocity and distance

H space equals space v over d

  • Therefore, as well as measurements of distance d to the Type 1a supernovae, measurements of red shift z are also needed

  • The recession velocities v of the Type 1a supernovae can be calculated from red shift using:

v space equals space z c

  • Values of red shift z can be obtained by measuring the wavelength of spectral lines from the Type 1a supernovae and comparing them to the same spectral lines from a source in a laboratory

Step 2: Describe how to plot the graph to determine the Hubble constant

  • Once the measurements of recession velocity v and distance d are obtained, they can be plotted on a graph with

    • velocity v, in km s-1, on the y-axis

    • distance d, in Mpc, on the x-axis

  • Then, the gradient of the graph is the Hubble constant H, in km s-1 Mpc-1

Step 3: Discuss any limitations in the obtained value of the Hubble constant

m space minus space M space equals space 5 space log space open parentheses d over 10 close parentheses

  • For Type 1a supernovae, the absolute magnitude M is known, but measurements of apparent magnitude m are required, which may be affected by light passing through gas and dust in space

  • A large amount of data is needed to reduce uncertainty, however, Type 1a supernovae are rare events, and their occurrence is difficult to predict

Other potential limitations:

  • There is a large variation in the data due to variations between galaxies or random errors in measurement

  • Type 1a supernovae are typically observed at large distances, where data suggests that the expansion of the Universe is accelerating, so this leads to discrepancies in values of H compared to nearer sources

Examiner Tips and Tricks

The units for the quantities in Hubble's law and the Hubble constant can change depending on the situation. Make sure you convert them to appropriate units and express your final answer correctly. 

The Hubble constant is given in the data booklet as H space equals space 65 space km space straight s to the power of negative 1 end exponent space Mpc to the power of negative 1 end exponent

To convert this into SI units:

  • Multiply by 1 km

  • Divide by 1 Mpc, where 1 parsec = 3.08 × 1016 m (from the data booklet)

H space equals space fraction numerator 65 cross times 10 cubed over denominator open parentheses 3.08 cross times 10 to the power of 16 close parentheses open parentheses 10 to the power of 6 close parentheses end fraction space equals space 2.1 cross times 10 to the power of negative 18 end exponent space straight s to the power of negative 1 end exponent

Estimating the Age of the Universe

  • Hubble’s Law is extremely important as it can give us an estimate the age of the Universe

  • It can be used to find the time since the expansion began, and hence the age of the Universe

  • We can calculate the time taken to reach a distant object from the Earth if we know 

    • how far away it is

    • its recessional speed

  • This requires a couple of assumptions:

    • all points in the Universe were initially together

    • the recessional speed of a galaxy is and has always been constant

  • Comparing the equation for speed, distance and time:

time space equals space distance over speed space equals space d over v

  • With the Hubble equation:

v space equals space H d space space space space space rightwards double arrow space space space space space H space equals space v over d

  • It can be seen that:

time space equals space 1 over H

  • If we consider that all matter was at the same point at the very start of the Big Bang (t = 0), then the time taken for the galaxy to expand to its current state must be equal to the age of the Universe

  • Using current estimations of the Hubble constant, astronomers believe that the universe has been expanding for around 13.7 billion years

Worked Example

In 2020, the best estimate for the Hubble constant was 67.4 km s−1 Mpc−1.

Use this value to calculate the age of the Universe.

Answer:

Step 1: List the known quantities

  • Hubble constant, H = 67.4 km s−1 Mpc−1

  • 1 parsec = 3.08 × 1016 m (from the data booklet)

  • 1 year = (60 × 60 × 24 × 365) = 3.15 × 107 s

Step 2: Convert the Hubble constant into SI units

  • First, multiply by 1 km, or 103 m

H space equals space 67.4 space km space straight s to the power of negative 1 end exponent space Mpc to the power of negative 1 end exponent space equals space 67.4 cross times 10 cubed space straight m space straight s to the power of negative 1 end exponent space Mpc to the power of negative 1 end exponent

  • Then, divide by 1 Mpc, or 3.08 × 1022 m

H space equals space fraction numerator 67.4 cross times 10 cubed space straight m space straight s to the power of negative 1 end exponent over denominator 3.08 cross times 10 to the power of 22 space straight m end fraction space equals space 2.19 cross times 10 to the power of negative 18 end exponent space straight s to the power of negative 1 end exponent

Step 3: Calculate the age of the Universe

  • The age of the Universe is equivalent to the reciprocal of the Hubble constant:

t space equals space 1 over H space equals space fraction numerator 1 over denominator 2.19 cross times 10 to the power of negative 18 end exponent end fraction space equals space 4.57 cross times 10 to the power of 17 space straight s 

t space equals space fraction numerator 4.57 cross times 10 to the power of 17 over denominator 3.15 cross times 10 to the power of 7 end fraction = 1.45 × 1010 years = 14.5 billion years

You've read 1 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

  • I would just like to say a massive thank you for putting together such a brilliant, easy to use website.I really think using this site helped me secure my top gradesin science and maths. You really did save my exams! Thank you.

    Beth
    IGCSE Student

  • This website is soooo useful and I can’t ever thank you enough for organising questions by topic like this. Furthermore, the name of the website could not have been more appropriate as it literally did SAVE MY EXAMS!

    Fathima
    A Level Student
Test yourself

Did this page help you?

Previous:Galactic RedshiftNext:Evidence for the Big Bang
Katie M

Author: Katie M

Expertise: Physics Content Creator

Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.

Download notes on Hubble's Law