Drawing Graphs from Tables (WJEC GCSE Maths & Numeracy (Double Award)): Revision Note
Exam code: 3320
Drawing graphs using a table
How do I draw a graph using a table of values?
To create a table of values
substitute different x-values into the equation
This gives the y-values
To plot the points
Use the x and y-values to mark crosses on the grid at the coordinates (x , y )
Each point is expected to be plotted to an accuracy within half of the smallest square on the grid
Draw a single smooth freehand curve
Go through all the plotted points
Make it the shape you would expect
For example, quadratic curves have a vertical line of symmetry
Do not use a ruler for curves!
Which numbers should I be careful with?
For quadratic graphs, be careful substituting in negative numbers
Always put brackets around them and use BIDMAS
For example, x = -3 in y = -x2 + 8x
becomes y = -(-3)2 + 8(-3)
which simplifies to -9 - 24
so y = - 33
How do I use the table function on my calculator?
Calculators can create tables of values for you
Find the table function
Type in the graph equation (called the function, f(x))
Use the alpha button then X or x
Press = when finished
If you are asked for another function, g(x), press = to ignore it
Enter the start value
The first x-value in the table
Press =
Enter the end value
The last x-value in the table
Enter the step size
How big the steps (gaps) are from one x-value to the next
Press =
Then scroll up and down to see all the y-values
Examiner Tips and Tricks
If you find a point that doesn't seem to fit the shape of the curve, check your working!
Worked Example
(a) Complete the table of values for the graph of .
|
|
|
|
|
Answer:
Use the table function on your calculator for
Start at -1.5, end at 1.5 and use steps of 0.5
On a non-calculator paper, substitute the x-values into the equation, for example x = -1.5
-8 | 8 | 10 | 8 | 2 |
(b) Plot the graph of on the axes below, for values of
from
to
.
Answer:
Carefully plot the points from your table on to the grid
Note the different scales on the axes
Join the points with a smooth curve (do not use a ruler)
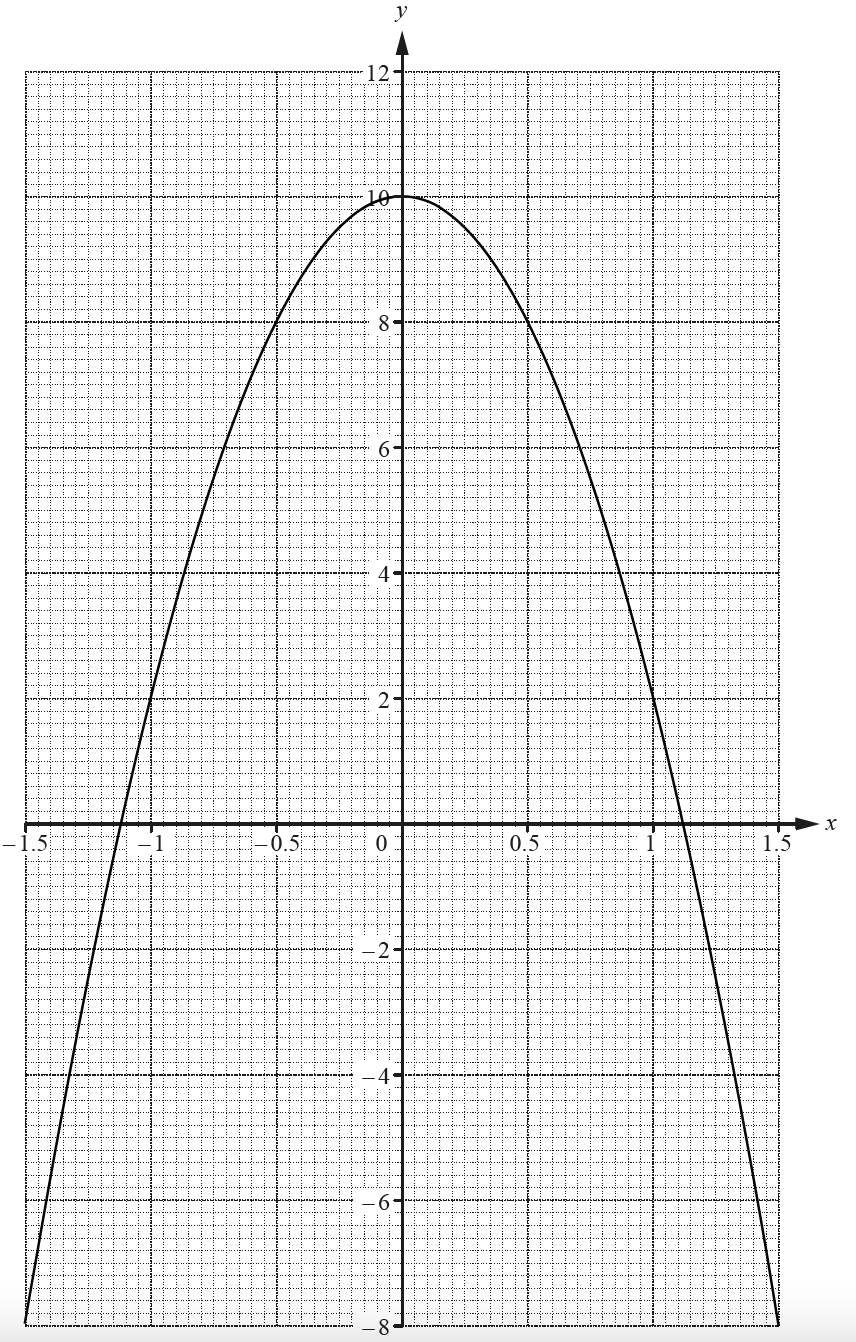
(c) Write down the equation of the line of symmetry of the curve.
Answer:
There is a vertical line of symmetry about the y-axis
The equation of the y-axis is x = 0
x = 0

Unlock more, it's free!
Was this revision note helpful?
