Transmission Diffraction Grating (OCR A Level Physics): Revision Note
Exam code: H556
Transmission Diffraction Grating
Dispersion is the separation of visible white light into a spectrum of its colours
This can be done using a glass prism or a diffraction grating
Transmission diffraction gratings are useful for separating light of different wavelengths with high resolution in order to:
Analyse light from stars
Analyse the composition of a star

Diffraction gratings are most commonly used in spectrometers to analyse light from stars
A transmission diffraction grating is a glass or plastic slide containing a large number of regularly spaced, parallel slits or lines
It is used to analyse spectral line wavelengths from the light emitted by stars
The angular dispersion (separation) of the colours is much greater using a transmission diffraction grating than an optical prism
Using diffraction gratings results in sharper fringes compared to using a double slit
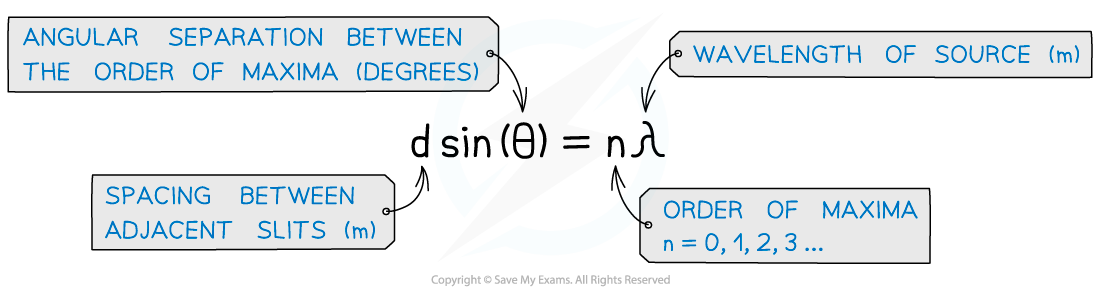
Condition for Maxima for a Diffraction Grating
The angles at which the maxima of intensity (constructive interference) are produced can be deduced by the diffraction grating equation:
Exam questions sometime state the lines per m (or per mm, per nm etc.) on the grating which is represented by the symbol N
d can be calculated from N using the equation
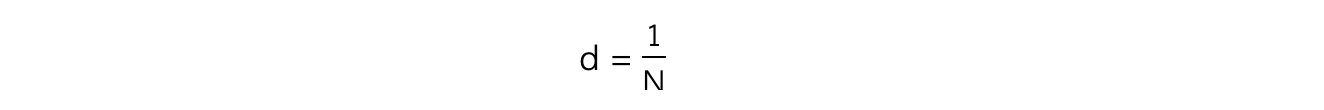
Angular Separation
The angular separation of each maxima is calculated by rearranging the grating equation to make θ the subject
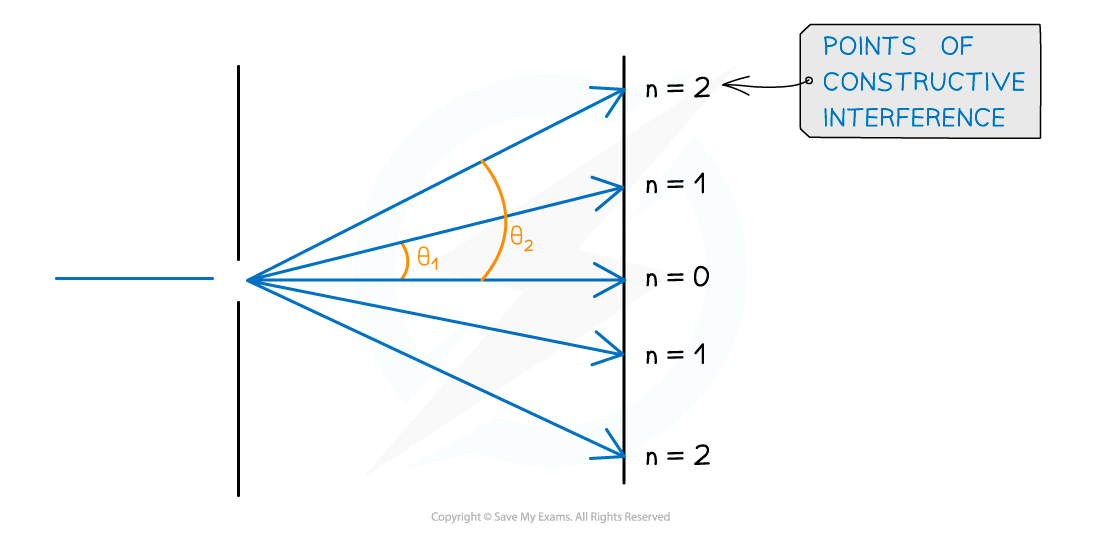
The angle θ is taken from the centre meaning the higher orders are at greater angles
Angular separation
The angular separation between two angles is found by subtracting the smaller angle from the larger one
The angular separation between the first and second maxima n1 and n2 is θ2 – θ1
Orders of Maxima
The maximum angle to see orders of maxima is when the beam is at right angles to the diffraction grating
This means θ = 90o and sin θ = 1
The highest order of maxima visible is therefore calculated by the equation:
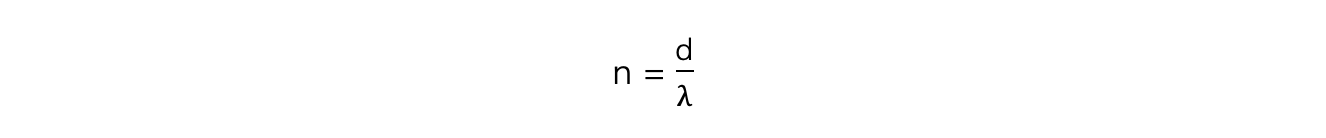
Note that since n must be an integer, if the value is a decimal it must be rounded down
E.g If n is calculated as 2.7 then n = 2 is the highest order visible
Worked Example
An experiment was set up to investigate light passing through a diffraction grating with a slit spacing of 1.7 µm. The fringe pattern was observed on a screen. The wavelength of the light is 550 nm.
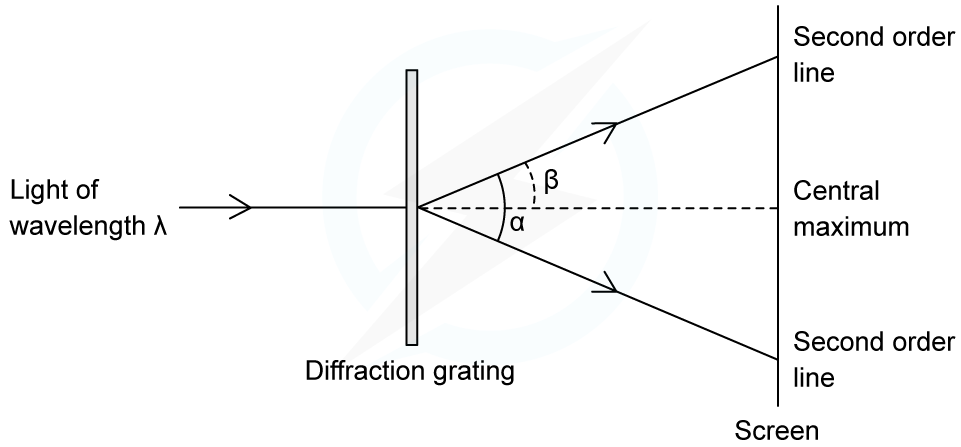
Calculate the angle α between the two second-order lines.
Answer:

Examiner Tips and Tricks
Take care that the angle θ is the correct angle taken from the centre and not the angle taken between two orders of maxima.

Unlock more, it's free!
Did this page help you?