Motion of Charged Particles in a B Field (OCR A Level Physics): Revision Note

Motion of a Charged Particle in a Magnetic Field

• A charged particle in uniform magnetic field which is perpendicular to its direction of motion travels in a circular path

• This is because the magnetic force F will always be perpendicular to its velocity v

  • F will always be directed towards the centre of the path in circular motion

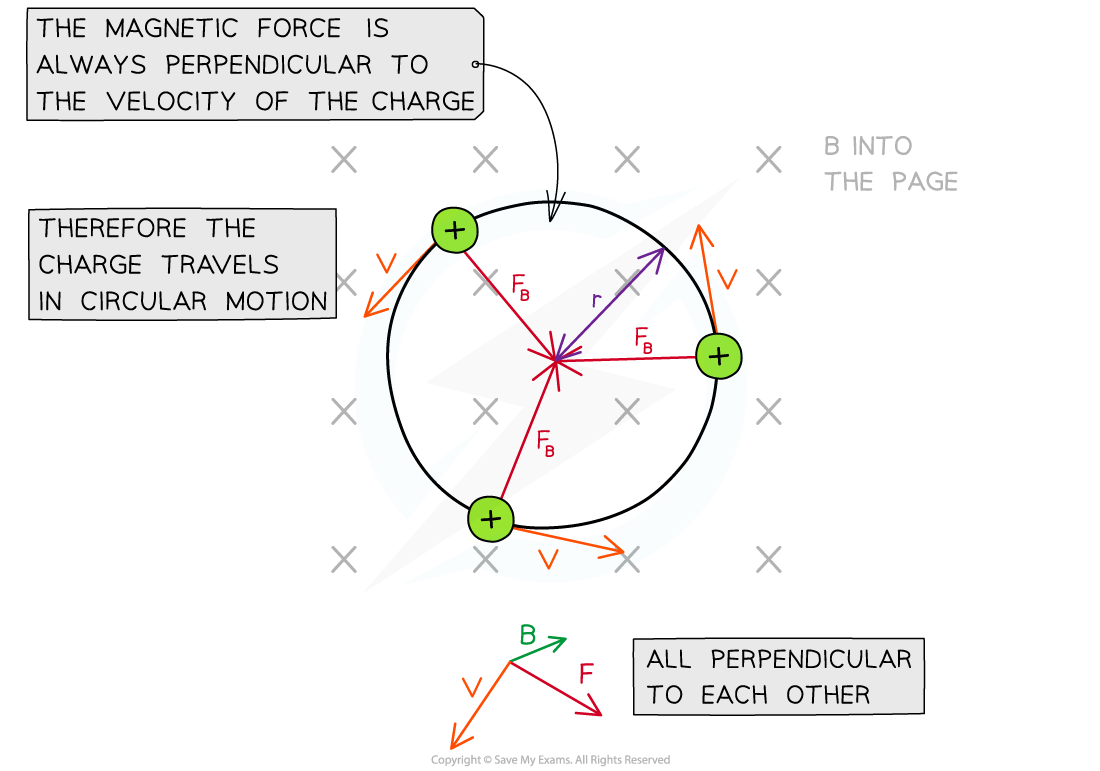
A charged particle moves travels in a circular path in a magnetic field

• The magnetic force F provides the centripetal force on the particle

• The equation for centripetal force is:

• Where:

  • F = centripetal force (N)

  • m = mass of the particle (kg)

  • v = linear velocity of the particle (m s⁻¹)

  • r = radius of the orbit (m)

• Equating this to the magnetic force on a moving charged particle gives the equation:

• Rearranging for the radius r obtains the equation for the radius of the orbit of a charged particle in a perpendicular magnetic field:

• This equation shows that:

  • Faster moving particles with speed v move in larger circles (larger r): r ∝ v

  • Particles with greater mass m move in larger circles: r ∝ m

  • Particles with greater charge q move in smaller circles: r ∝ 1 / q

  • Particles moving in a strong magnetic field B move in smaller circles: r ∝ 1 / B

• The centripetal acceleration is in the same direction as the centripetal (and magnetic) force

  • This can be found using Newton's second law:

F = ma