AP®MathsCollege BoardCalculus ABStudy GuidesUnit 2: Differentiation Definition & Fundamental PropertiesDefinition of DifferentiationDifferentiability & Continuity

Differentiability & Continuity (College Board AP® Calculus AB): Study Guide

Jamie Wood

Written by: Jamie Wood

Reviewed by: Dan Finlay

Updated on

College Board Calculus ABCollege Board Calculus BC

Differentiability & continuity

When is a function differentiable?

  • The derivative of a function is defined as f to the power of apostrophe open parentheses x close parentheses equals limit as h rightwards arrow 0 of space fraction numerator f open parentheses x plus h close parentheses minus f open parentheses x close parentheses over denominator h end fraction

    • The derivative only exists if this limit exists

    • The derivative, if it exists, is itself a function

  • If a point is not in the domain of f open parentheses x close parentheses then it cannot be in the domain of f apostrophe open parentheses x close parentheses

    • This means f open parentheses x close parentheses will not be differentiable at points where there is a vertical asymptote

      • E.g. f open parentheses x close parentheses equals 1 over x is not differentiable at x equals 0

  • A differentiable function is one for which its derivative exists at each point in its domain

    • This means that a function with points at which it is not differentiable can still be made a differentiable function by appropriately restricting its domain

  • A function must be continuous at a point to be differentiable at that point

    • Therefore if a function is differentiable at a point, then it is continuous at that point

    • And if a function is not continuous at a point, then it is not differentiable at that point

  • However, if a function is continuous at a point, it is not necessarily differentiable at that point

    • A continuous function may contain a point at which it is not differentiable

    • E.g. f open parentheses x close parentheses equals vertical line x vertical line is continuous at x equals 0, but it is not differentiable at x equals 0

Examiner Tips and Tricks

Exam questions often state that a function is differentiable, and expect you to know (and use the fact) that this automatically means the function is continuous as well

If a function is said to be twice differentiable, this means that the function's derivative is also continuous!

How can I show a function is not differentiable at a point?

  • If a function is not continuous at a point, then it is not differentiable at that point

    • That's the easiest way to show a function is not differentiable at a point!

  • If a function is continuous at a point, then to show it is not differentiable

    • you need to go back to the limit definition of the derivative

      • f to the power of apostrophe open parentheses x close parentheses equals limit as h rightwards arrow 0 of space fraction numerator f open parentheses x plus h close parentheses minus f open parentheses x close parentheses over denominator h end fraction

  • Recall that the limit of a function does not exist if the function inside the limit

    • is unbounded at the point in question

    • oscillates near the point in question

    • or has unequal one-sided limits at the point in question

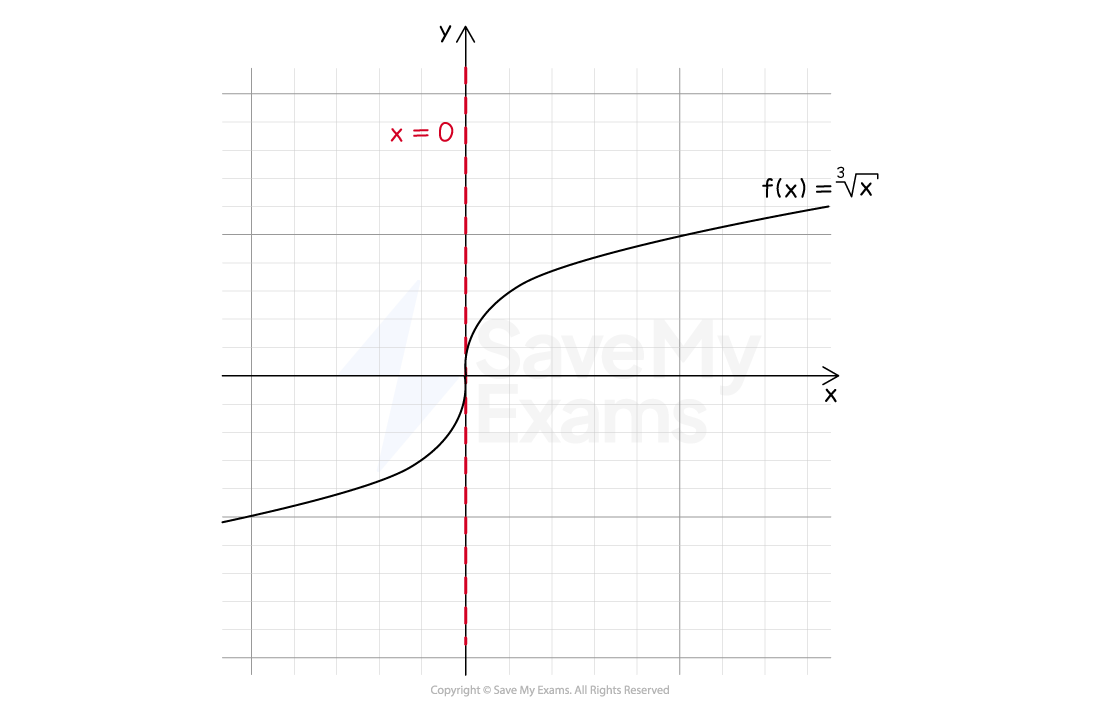
  • Consider the graph of y equals vertical line x vertical line shown below

Graph of y=|x|

  • At (0, 0), f open parentheses x close parentheses equals open vertical bar x close vertical bar is not differentiable

  • To show why, consider the derivative at (0, 0)

    • f to the power of apostrophe open parentheses 0 close parentheses equals limit as h rightwards arrow 0 of space fraction numerator f open parentheses 0 plus h close parentheses minus f open parentheses 0 close parentheses over denominator h end fraction equals limit as h rightwards arrow 0 of space fraction numerator open vertical bar h close vertical bar minus open vertical bar 0 close vertical bar over denominator h end fraction equals limit as h rightwards arrow 0 of space fraction numerator open vertical bar h close vertical bar over denominator h end fraction

  • Consider the one-sided limit from the left

    • For h less than 0, fraction numerator open vertical bar h close vertical bar over denominator h end fraction equals fraction numerator negative h over denominator h end fraction equals negative 1

    • So limit as h rightwards arrow 0 to the power of minus of space fraction numerator open vertical bar h close vertical bar over denominator h end fraction equals limit as h rightwards arrow 0 to the power of minus of space open parentheses negative 1 close parentheses equals negative 1

  • Consider the one-sided limit from the right

    • For h greater than 0, fraction numerator open vertical bar h close vertical bar over denominator h end fraction equals h over h equals 1

    • So limit as h rightwards arrow 0 to the power of plus of space fraction numerator open vertical bar h close vertical bar over denominator h end fraction equals limit as h rightwards arrow 0 to the power of plus of open parentheses 1 close parentheses equals 1

  • You can also see this visually from the graph

    • The slope for negative values of x is -1

    • The slope for positive values of x is 1

  • The one-sided limits do not agree, therefore the limit f apostrophe open parentheses x close parentheses equals limit as h rightwards arrow 0 of space fraction numerator f open parentheses x plus h close parentheses minus f open parentheses x close parentheses over denominator h end fraction at (0, 0) does not exist

    • Therefore f open parentheses x close parentheses equals open vertical bar x close vertical bar is not differentiable at (0, 0)

Examiner Tips and Tricks

If you have to explain why a derivative does not exist at a point where a function is continuous:

  • use the limit definition of a derivative, f apostrophe open parentheses x close parentheses equals limit as h rightwards arrow 0 of space fraction numerator f open parentheses x plus h close parentheses minus f open parentheses x close parentheses over denominator h end fraction

  • and show that the limit does not exist

Where else might a graph not be differentiable?

  • If the graph of a function has a point where the tangent to the graph is vertical, then the derivative is undefined at that point

    • E.g. at x equals 0 on the graph of f open parentheses x close parentheses equals cube root of x

    • The limit in the limit definition of the derivative would become unbounded at such a point

Graph of cube root of x, with a vertical tangent at x=0

Worked Example

Let f be the function defined by f open parentheses x close parentheses equals square root of open vertical bar x plus 6 close vertical bar end root for all x. Which of the following statements is true?

(A) x equals negative 6 is a vertical asymptote of the graph of f.

(B) f is not continuous at x equals negative 6.

(C) limit as x rightwards arrow negative 6 of f open parentheses x close parentheses not equal to 0

(D) f is continuous but not differentiable at x equals negative 6.

Answer:

Consider option (A)

There will be a vertical asymptote if the function becomes unbounded at this point

Check by substituting in x equals negative 6

f open parentheses negative 6 close parentheses equals square root of open vertical bar negative 6 plus 6 close vertical bar end root equals square root of 0 equals 0

The function has a well-defined value of 0 at x equals negative 6, so there is not an asymptote

Consider option (B)

We have already checked the value of the function at x equals negative 6 and it has a value of 0

The limits from the left and right at x equals negative 6 are also equal to 0 (see below)

Therefore the function is continuous at x equals negative 6

Consider option (C)

Check the one-sided limit from the left using substitution

limit as x rightwards arrow open parentheses negative 6 close parentheses to the power of minus of square root of open vertical bar x plus 6 close vertical bar end root equals square root of open vertical bar open parentheses negative 6 close parentheses plus 6 close vertical bar end root equals square root of 0

Check the one-sided limit from the right using substitution

limit as x rightwards arrow open parentheses negative 6 close parentheses to the power of plus of square root of open vertical bar x plus 6 close vertical bar end root equals square root of open vertical bar open parentheses negative 6 close parentheses plus 6 close vertical bar end root equals square root of 0

The two one-sided limits agree therefore limit as x rightwards arrow negative 6 of square root of open vertical bar x plus 6 close vertical bar end root equals 0

Consider option (D)

By elimination the answer is D, but we can also check this by inspecting the graph of f open parentheses x close parentheses

You could use your graphing calculator to do this

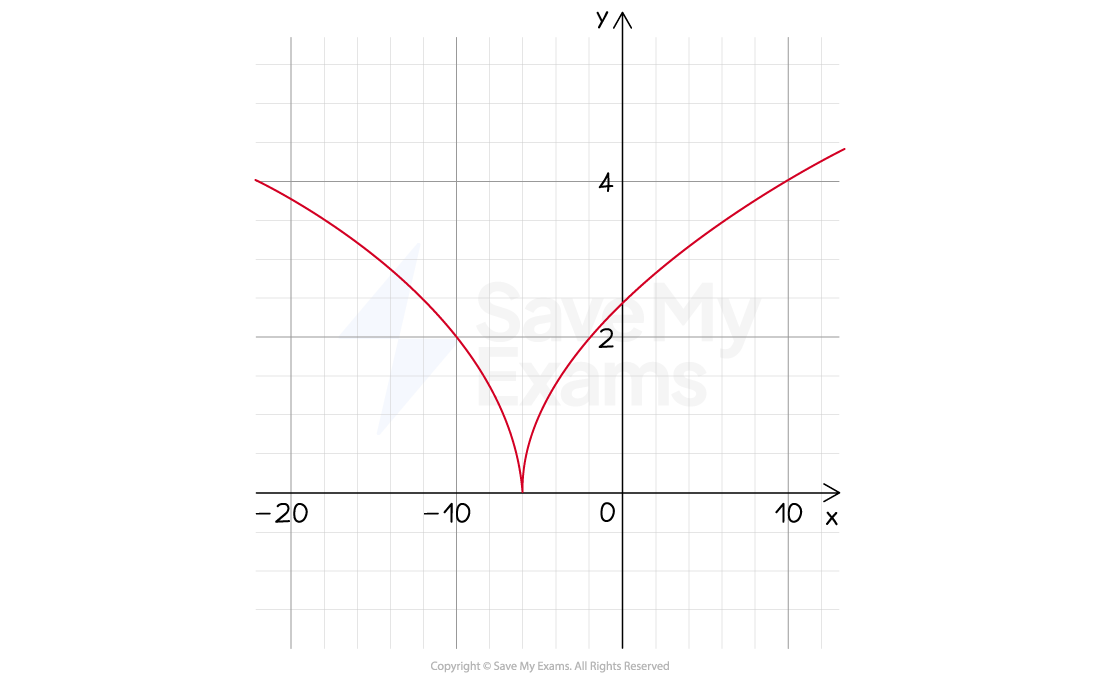
graph of square root of (mod (x+6))

It can be seen that there is a cusp at (-6,0) so at this point the function is continuous, but not differentiable

Option (D)

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself
    Previous:Estimating the Derivative at a PointNext:Derivative Rules
    Author
    Reviewer
    Jamie Wood

    Author: Jamie Wood

    Expertise: Maths Content Creator

    Jamie graduated in 2014 from the University of Bristol with a degree in Electronic and Communications Engineering. He has worked as a teacher for 8 years, in secondary schools and in further education; teaching GCSE and A Level. He is passionate about helping students fulfil their potential through easy-to-use resources and high-quality questions and solutions.

    Dan Finlay

    Reviewer: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.