Investigating Circular Motion (OCR A Level Physics): Revision Note

Investigating Circular Motion

Equipment & Method

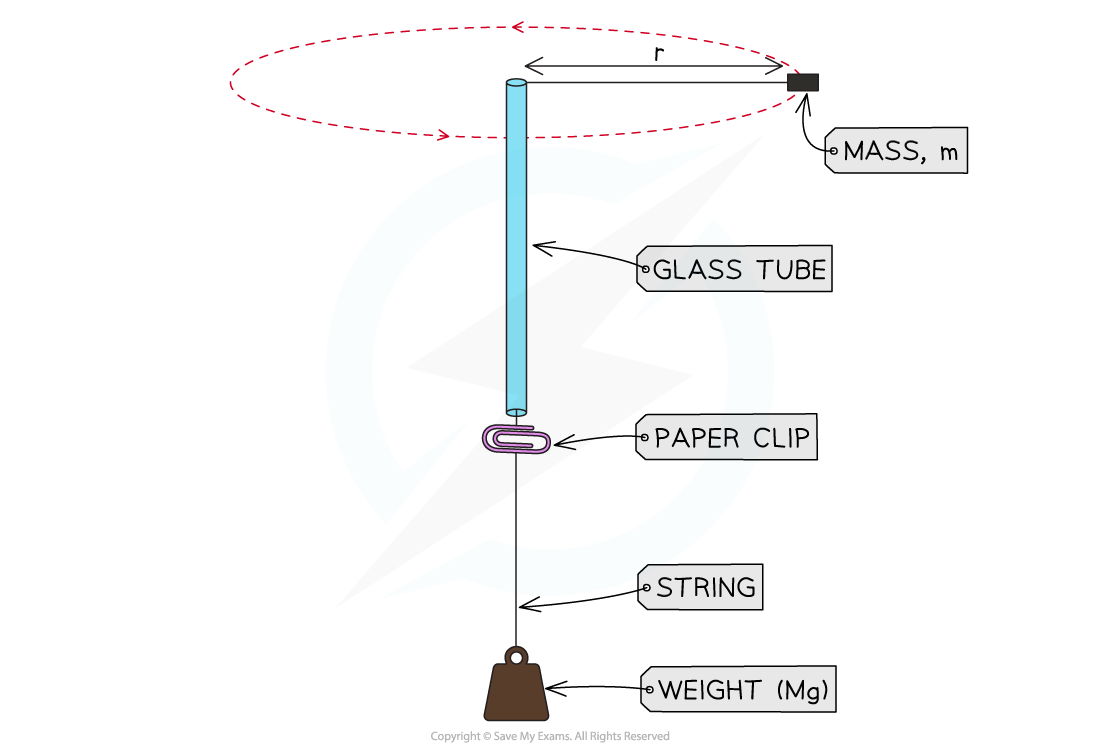
• Circular motion can be investigated using the following setup:

  • Tie a bung of mass m, to a piece of string, which sits horizontally

  • Thread it though a glass tube and a paper clip, which sits vertically

  • At the other end of the string an object with mass M is suspended vertically (a mass or some washers are commonly used)

  • This weight creates constant tension in the string and provides the centripetal force

  • The paperclip acts as a marker; the speed of the rotation is adjusted until the paperclip remains in a fixed position just below the glass tube

  • The string is spun in a horizontal circle

  • The period of the rotation is measured

    • The time taken for multiple rotations is recorded and repeated to reduce random errors

  • The experiment is repeated again using different distances between the mass and the glass tube (the radius of the circle)

Explanation

• The weight force Mg exerted on the string by the hanging mass M creates tension in the string

  • The centripetal force should be found to be approximately equal to this weight force

• The angular velocity of the bung, mass m, can be found using

• Where:

  • = angular velocity (rad s^-1)

  • = time period of oscillation (s)

• The centripetal force can be calculated using

• Where:

  • = centripetal force (N)

  • = mass of bung (kg)

  • = angular velocity (rad s^-1)

  • = radius of circle = length of string between bung and glass tube (m)

• The centripetal force should be found to be approximately equal to the weight of the hanging mass,

• Where:

  • = mass of the hanging mass providing the tension in the string (kg)

  • = gravitational field strength (N kg^-1)

• The investigation should show that as increases, the time period increases, but the centripetal force remains the same