Polynomial Functions (DP IB Analysis & Approaches (AA)): Revision Note

Sketching polynomial graphs

What is a polynomial?

• A polynomial is a sum of terms of the form where

  • is a real number

  • is an integer

• A polynomial looks like

• The degree of a polynomial is its highest power

  • e.g. the degree of is 3

  • e.g. the degree of is 1

• The leading term of a polynomial is the term with the highest power

  • e.g. the leading term of is

What’s the relationship between a polynomial’s degree and its zeros?

• If a real polynomial has degree n

  • it will have n zeros which can be written in the form , where

    • these zeros are not necessarily distinct

    • they can be repeated

• For example:

  • A quadratic will have 2 zeros

  • A cubic function will have 3 zeros

  • A quartic will have 4 zeros

• Every real polynomial of odd degree has at least one real zero

What do I need to know to sketch the graph of a polynomial function?

• Suppose  is a real polynomial with degree n

• To sketch the graph of a polynomial you need to know three things:

  • The y-intercept

    • Find this by substituting x = 0 to get

  • The roots

    • You can find these by factorising or solving y = 0

  • The shape

    • This is determined by the degree (n) and the sign of the leading coefficient ()

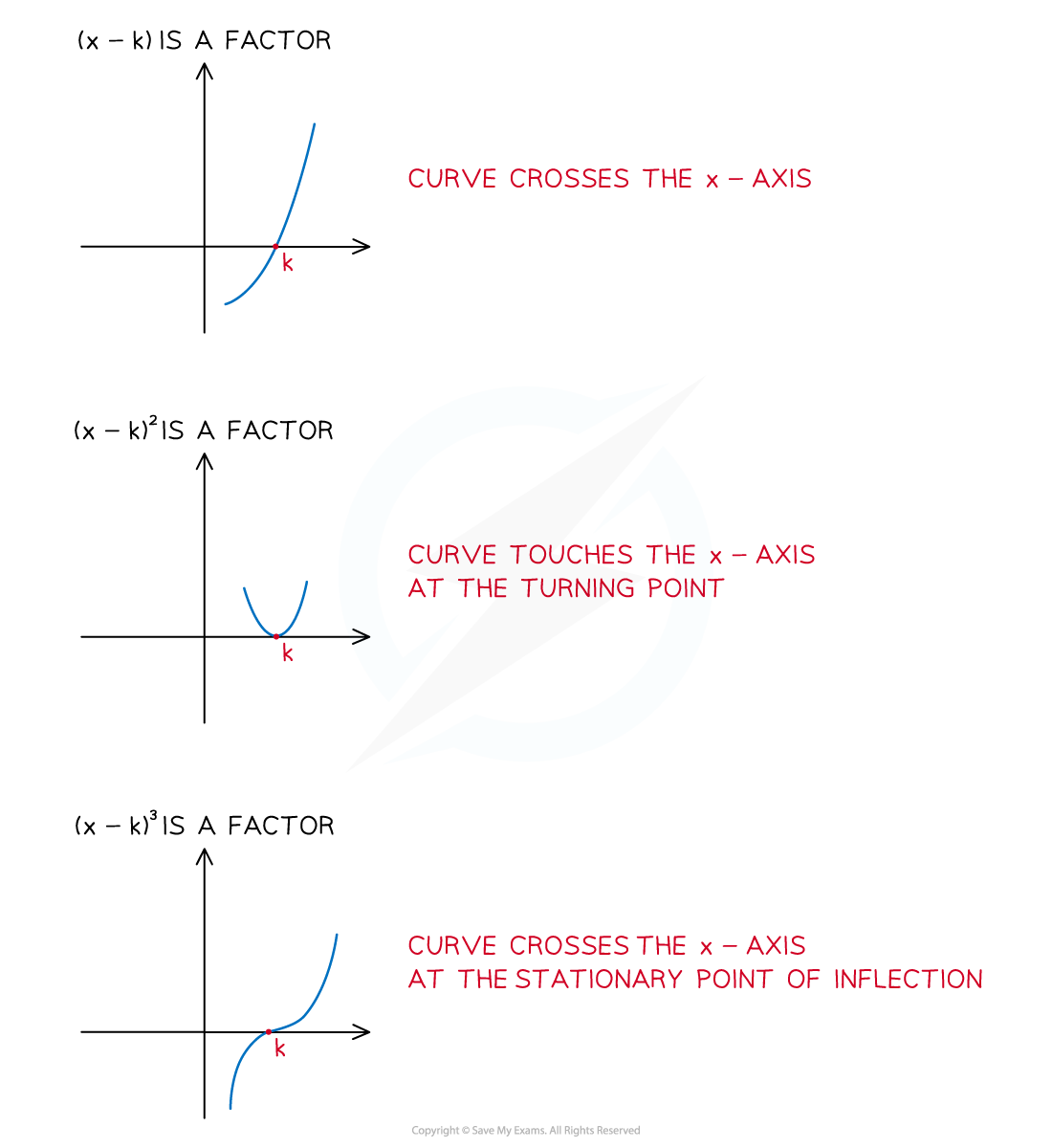
How does the multiplicity of a real root affect the graph of the polynomial?

• The multiplicity of a root is the number of times it is repeated when the polynomial is factorised

  • If  is a root with multiplicity m then  is a factor of the polynomial

• The graph either crosses the x-axis or touches the x-axis at a root x = k where k is a real number

  • If has multiplicity 1 then the graph crosses the x-axis at

  • If has multiplicity 2 then the graph has a turning point at so touches the x-axis 

    • If has odd multiplicity m ≥ 3 then the graph has a stationary point of inflection at so crosses the x-axis

    • If has even multiplicity m ≥ 4 then the graph has a turning point at so touches the x-axis

How do I determine the shape of the graph of the polynomial?

• Consider what happens as x tends to ± ∞

How do I sketch the graph of a polynomial function?

• Plot the y-intercept

• Plot the roots

• Identify the multiplicity of each root

• Identify where the graph starts and ends

• Connect the points using a smooth curve

• There will be at least one turning point in-between each pair of roots

  • If the degree is n then there is at most n – 1 stationary points

    • Every real polynomial of even degree has at least one turning point

    • Every real polynomial of odd degree bigger than 1 has at least one point of inflection

Solving polynomial equations

What is “The Fundamental Theorem of Algebra”?

• Every real polynomial with degree n can be factorised into n complex linear factors

  • Some of which may be repeated

  • This means the polynomial will have n zeros (some may be repeats)

• Every real polynomial can be expressed as a product of real linear factors and real irreducible quadratic factors

  • An irreducible quadratic is where it does not have real roots

    • The discriminant will be negative: b² – 4ac < 0

• If a + bi (b ≠ 0) is a zero of a real polynomial

  • then its complex conjugate a – bi is also a zero

• Every real polynomial of odd degree will have at least one real zero

How do I solve polynomial equations?

• Suppose you have an equation where is a real polynomial of degree n

  • 

• You may be given one zero or you might have to find a zero x = k by substituting values into P(x) until it equals 0

• If you know a root then you know a factor

  • If you know x = k is a root then (x – k) is a factor

  • If you know x = a + bi is a root then you know a quadratic factor (x – (a + bi))( x – (a – bi))

    • Which can be written as ((x – a) - bi)((x – a) + bi) and expanded quickly using difference of two squares

• You can then divide P(x) by this factor to get another factor

  • For example: dividing a cubic by a linear factor will give you a quadratic factor

• You then may be able to factorise this new factor