Applying General Mathematics in Physics (DP IB Physics): Revision Note

Written by: Katie M

Reviewed by: Caroline Carroll

Updated on 17 October 2025

Algebra & mathematical relationships

Using arithmetic and algebraic calculations in physics

Solving problems with algebra is a fundamental skill in physics
This involves:
- applying the laws of arithmetic to algebraic expressions, i.e. addition, subtraction, multiplication, and division
- manipulating expressions algebraically to isolate variables
Example:
- Rearrange the following for $t$ :

$v = u + a t$

$v - u = a t$

$t = \frac{v - u}{a}$

Areas and volumes

You will often need to use formulas for simple shapes
- Note: The majority of these are included in the data booklet
Areas of simple shapes:
- Rectangle: $A = l w$
- Triangle: $A = \frac{1}{2} b h$
- Circle: $A = π r^{2}$
Volumes of simple shapes:
- Cuboid: $V = l w h$
- Cylinder: $V = π r^{2} h$
- Sphere: $V = \frac{4}{3} π r^{3}$
Other:
- Circumference of a circle: $C = 2 π r$
- Lateral (curved) surface area of a cylinder: $A = 2 π r h$
- Surface area of a sphere: $A = 4 π r^{2}$
Example:
- Density of a cylindrical wire of mass $m$ , radius $r$ , and length $L$ :

$ρ = \frac{m}{V}$

$ρ = \frac{m}{π r^{2} L}$

Decimals, fractions, percentages and ratios

Decimals
- Most physics calculations use decimals
Fractions
- These are most commonly used in algebra and uncertainty calculations
- Most scientific calculators will initially give answers as fractions
  - Make sure you know where the S⇔D button is so that you convert the fraction into a decimal
Percentages
- There are many percentage calculations, percentage change, percentage difference, percentage error and percentage uncertainty
Ratios
- These are commonly used to compare quantities
- Examples: efficiency, uncertainties

Reciprocals and exponents

Reciprocals
- The reciprocal of a number is the result of dividing 1 by that number
- Example:

$T = \frac{1}{f}$

Exponents
- An exponent is a power that a number is raised to
- Example:

$a = - ω^{2} x$

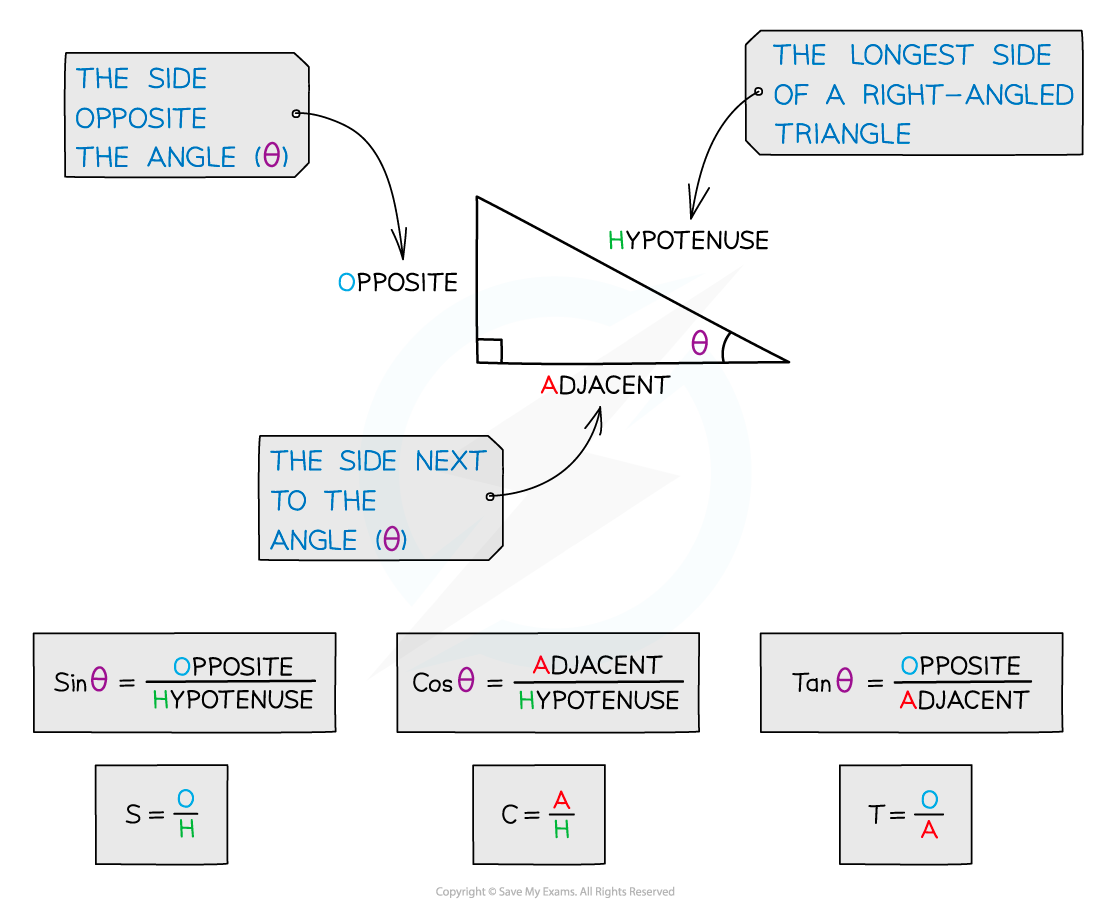
Trigonometric ratios

Many problems (e.g. vectors) in physics involve right-angled triangles
The functions sine, cosine and tangent are the ratios of the lengths of the sides of the triangle
sine:

$\sin θ = \frac{opposite}{hypotenuse} = \frac{O}{H}$

cosine:

$\cos θ = \frac{adjacent}{hypotenuse} = \frac{A}{H}$

tangent:

$\tan θ = \frac{opposite}{adjacent} = \frac{O}{A}$

Trigonometric formulae for a right-angled triangle

Logarithmic and exponential functions

Exponential change occurs when the rate of change of a quantity is proportional to its current value
- It can be an increase (e.g. population growth) or a decrease (e.g. radioactive decay)
An exponential function has the form:

$y = a^{x}$

A logarithm is the inverse function of an exponential function:
- $y = a^{x}$ becomes:

$\log y = x \log a$

Determine rates of change

The rate of change of a quantity is a measure of how quickly it changes with respect to time
The symbol $∆$ is used to represent a change in a quantity
For example, a change in temperature:

$∆ T = T_{f} - T_{i}$

Where
- $T_{f}$ = the final temperature
- $T_{i}$ = the initial temperature
From tabulated data, you can use the average rate of change, or gradient if the data has been plotted as a graph
The average rate of change between two points on a graph of $y$ against $x$ is:

rate of change = $\frac{∆ y}{∆ x}$

This is equivalent to the gradient of the graph when time is plotted on the x-axis

Calculate the mean and range

Mean

The mean average is often just called the “average”
It is the total of all the values divided by the number of values, i.e. add all the numbers together and divide by how many there are

Range

The range can only be applied to numerical data
It is a measure of how spread out the data is, which means that it is the difference between the highest and lowest values
It can be expressed as:
- a range of values
  - e.g. 9.2 - 8.4
- a single value
  - e.g. 9.2 - 8.4 = 0.8
The range can be affected when the highest and/or lowest data are anomalous results themselves

Equations and derivations in physics

As a physics student, you are not expected to memorise the various constants and equations, as these are provided in the data booklet
However, you will be assessed on your ability to
- select appropriate equations based on the physical situation
- manipulate equations algebraically to solve for a required variable
- derive relationships between variables

Select and manipulate equations

The ability to select the correct equation for a given context takes practice
To solve calculation questions quickly and efficiently:
- List all the known quantities, including their symbols
- Identify the equation in the data booklet that connects them
- If required, rearrange the equation for the quantity you're trying to calculate
- Substitute the known values into the equation and calculate the final answer

Worked Example

A car travelling at a constant velocity covers a distance of 50 m in 2.5 s. The thrust of the engine is 1.5 kN.

Calculate the power of the car.

Answer:

Step 1: List the known quantities

Distance, $s$ = 50 m
Time, $∆ t$ = 2.5 s
Force, $F$ = 1.5 kN = 1500 N

Step 2: Select the correct equations from the data booklet

Two equations are given for power, $P = \frac{∆ W}{∆ t}$ and $P = F v$
From the context, we are given force $F$ , distance $s$ , and time $∆ t$
Therefore, to calculate power, we can use
- either $P = \frac{∆ W}{∆ t}$ with the equation for work done $W = F s$
- or $P = F v$ with the equation for velocity $v = \frac{∆ s}{∆ t}$

Step 3: Manipulate the equations to obtain the correct form

$P = \frac{∆ W}{∆ t} = \frac{F s}{∆ t}$

Step 4: Substitute the values into the equation to obtain the final result

$P = \frac{F s}{∆ t} = \frac{1500 \times 50}{2.5} = 30 000 W$

Derive relationships algebraically

Deriving equations is a critical skill which tests your understanding of fundamental principles of physics to explain the origin of an equation
To tackle derivation questions
- Start by identifying the fundamental physical principle underlying the given context, e.g. forces, energy conservation, momentum
- List any equations from the data booklet you feel are relevant
- Combine and manipulate equations to construct a new equation
- If it is a "show that" question, you will be given the final form of the equation, so you just need to manipulate the algebra until you reach the required form

Worked Example

In Millikan's oil drop experiment, a charged spherical oil drop is stationary in the space between two parallel charged plates. The electric field strength between the plates is $E$ .

Show that the electric charge on the oil drop is given by

$q = \frac{4 π ρ g r^{3}}{3 E}$

where $ρ$ is the density of oil and $r$ is the radius of the oil drop.

Answer:

Step 1: Select the relevant questions from the data booklet

The fundamental physics principle is the relationship between two forces acting on the oil drop
- the electric force, $E = \frac{F}{q}$
- the gravitational force (weight), $F_{g} = m g$
We also need to use the following equations
- Density, $ρ = \frac{m}{V}$
- Volume of a sphere, $V = \frac{4}{3} π r^{3}$

Step 2: Use clues from the question to set up the derivation

The oil drop is stationary, which means the net force on it is zero
Therefore, the electric force = gravitational force

$F = E q = m g$

The oil drop is spherical and has radius $r$ and density $ρ$
Therefore, the mass of the oil drop is

$m = ρ V = \frac{4}{3} π ρ r^{3}$

Step 3: Manipulate the equations algebraically to obtain the final result

Substitute the expression for $m$ into the force equation

$E q = (\frac{4}{3} π ρ r^{3}) g$

Rearrange to isolate $q$ on the left-hand side of the equation

$q = \frac{4 π ρ g r^{3}}{3 E}$

Examiner Tips and Tricks

Always read the question carefully, highlighting any key words and phrases which might help you solve the problem, such as
- stationary or starts from rest
  - This means initial speed is zero, $u$ = 0
  - e.g. "The tennis ball was stationary at the instant when it was hit"
- constant speed or velocity
  - This means net force and acceleration are zero, $F_{n e t}$ = 0 and $a$ = 0
  - e.g. "A car travelling at a constant velocity"
- rebounds in the opposite direction
  - This means the sign of the velocity changes, $∆ v = v - (- u) = v + u$
  - e.g. "The ball hits a vertical wall and rebounds in the opposite direction"

Continuous and discrete variables

Variables can be quantitative (measurable) or qualitative (observable only)
Quantitative variables can also be
- Discrete
  - can only take certain values
  - data that is counted (rather than measured) and given as whole numbers
  - e.g. number of particles
- Continuous
  - can take any value
  - data that is measured and can be given as decimals or fractions
  - e.g. speed, time, mass

Direct and inverse proportionality

There are a number of terms that are commonly applied to trends, particularly in graphs
Directly proportional
- This applies to a trend that has a clear linear relationship
- Mathematically, this can be described as $y = k x$ , where $k$ is a constant which can be positive or negative
- In most situations, it is clear that $k$ is positive
- This means that the relationship can be described as "when one variable increases, the other increases" or "if $x$ doubles, then $y$ doubles"
- A directly proportional relationship is always a straight line through the origin with a fixed gradient
Inversely proportional
- This can be described as $y = \frac{k}{x}$ , where $k$ is a constant which can be positive or negative
- This means that the relationship can be described as "when one variable increases, the other decreases" or "if $x$ doubles, then $y$ halves"
- When plotted, inverse proportionality is not a straight line and does not pass through the origin
Positive correlation
- This term is best applied to the gradient of a graph
- The gradient of the graph is positive / slopes or curves upwards
- It describes a relationship where, as $x$ increases, $y$ also increases
Negative correlation
- This term is also best applied to the gradient of a graph
- The gradient of the graph is negative / slopes or curves downwards
- It describes a relationship where as $x$ increases, $y$ decreases

Examiner Tips and Tricks

Careful: A common mistake made by students is to describe any graph with a straight line going diagonally upwards as directly proportional
- This is not correct because direct proportionality must go through the origin
- A graph that does not go through the origin can correctly be described as proportional, but it is not directly proportional

Determine the effect of changing variables

In physics, you will often use algebra to determine how a change in one variable affects another variable
- For example, Charles' law states that for a fixed amount of gas at constant pressure, volume and temperature are proportional, $V \propto T$
- Therefore, if the volume changes from $V_{1}$ to $V_{2}$ , and the temperature changes from $T_{1}$ to $T_{2}$ , then we can represent this change as a ratio

$\frac{V_{1}}{T_{1}} = \frac{V_{2}}{T_{2}}$

Many questions can be solved in this way using ratios and proportionality
- Identify the equation linking the variables
- Rearrange for the variable of interest, if required
- Write the equation as a ratio, eliminating any constants
- Substitute initial and final values and calculate

Worked Example

A cylinder of copper with cross-sectional area $A$ and length $L$ has a resistance $R$ .

What is the resistance of a copper cylinder with cross-sectional area $\frac{A}{2}$ and length $2 L$ ?

Answer:

Step 1: Identify the equation linking the variables

The equation linking area $A$ , length $L$ , and resistance $R$ is resistivity:
- $ρ = \frac{R A}{L}$

Step 2: Rearrange for the variable of interest, resistance

$ρ = \frac{R A}{L} \to R = \frac{ρ L}{A}$

Step 3: Write the equation as a ratio and eliminate any constants

The resistivity of copper is a constant
Resistance changes from $R_{1} = R$ to $R_{2}$
Length changes from $L_{1} = L$ to $L_{2} = 2 L$
Cross-sectional area changes from $A_{1} = A$ to $A_{2} = \frac{A}{2}$

$R \propto \frac{L}{A}$

$\frac{R_{1}}{R_{2}} = \frac{L_{1} / A_{1}}{L_{2} / A_{2}} = (\frac{L_{1}}{L_{2}}) (\frac{A_{2}}{A_{1}})$

Step 4: Substitute initial and final values and calculate

$\frac{R_{1}}{R_{2}} = (\frac{L}{2 L}) (\frac{A}{2 A}) = \frac{1}{4}$

$R_{2} = 4 R_{1}$

Percentage change and percentage difference

Percentage change and percentage difference are commonly used to express the relative change between two values
- They are useful for comparing experimental results

Percentage change

Percentage change is used to express the relative change between an initial value and a final value
It is calculated using the following formula:

percentage change = $\frac{final value - initial value}{initial value} \times 100$

Percentage difference

Percentage difference is used to compare two values to determine how much they differ from each other as a percentage
It is calculated using the following formula:

percentage difference = $\frac{value 1 - value 2}{(average of value 1 and value 2)} \times 100$

Percentage error

Percentage error is used to express the difference between an experimental value and an accepted or literature value
- It is not a percentage uncertainty

The percentage error is defined by the equation:

percentage error = $\frac{accepted value - experimental value}{accepted value} \times 100$

The experimental value is sometimes referred to as the 'measured' value
The accepted value is sometimes referred to as the 'true' value
- This may be labelled on a component, such as the resistance of a resistor
- Or, from a reputable source such as a peer-reviewed data booklet

For example, the acceleration due to gravity g is known to be 9.81 m s^–2. This is its accepted value
- From an experiment, the value of g may be found to be 10.35 m s^–2
- Its percentage error would therefore be 5.5 %
The smaller the percentage error, the more accurate the results of the experiment

Percentage uncertainty

Percentage uncertainties are a way to compare the significance of an absolute uncertainty on a measurement
- This is not to be confused with percentage error, which is a comparison of a result to a literature value
Percentage uncertainty is calculated using the following formula

percentage uncertainty = $\frac{absolute uncertainty}{measured value} \times 100$

Scientific notation & significant figures

What is scientific notation?

Scientific notation is also known as standard form
It is a system of writing and working with very large or very small numbers
- For example, Avogadro's number 602 000 000 000 000 000 000 000 is 6.02 × 10²³ in scientific notation
Numbers in scientific notation are written as:

a × 10ⁿ

They follow these rules:
- a is a number above 1 and below 10
- For large numbers, n is an integer that is greater than 0
  - i.e. it shows how many times a is multiplied by 10
- For small numbers, n is an integer that is less than 0
  - i.e. it shows how many times a is divided by 10

Applying scientific notation to numbers

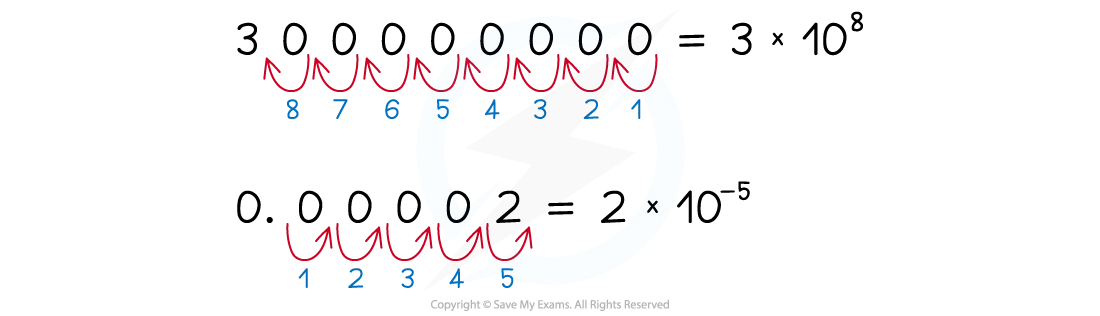
Diagram showing how to convert large and small numbers into scientific notation — **The scientific notation for numbers greater than 1 has the × 10 raised to a positive power while the scientific notation for numbers less than 1 has the × 10 raised to a negative power**

When rounding a number in standard form to a certain number of significant figures, only the value of a is rounded (the × 10ⁿ value will not be significant)
- For example, 4.37 × 10⁶ to 2 significant figures is 4.4 × 10⁶

Significant figures

Significant figures are the digits used to represent a given quantity
Significant figures describe the precision to which a quantity is known
- The more precise a measurement, the greater the number of significant figures that can be used to represent it
There are some important rules to remember for significant figures
- All non-zero digits are significant
- Zeros between non-zero digits are significant
  - 4107 (4 s.f.)
  - 29.009 (5 s.f.)
- Zeros that come before all non-zero digits are not significant
  - 0.00079 (2 s.f.)
  - 0.48 (2 s.f.)
- Zeros after non-zero digits within a number without decimals are not significant
  - 57 000 (2 s.f.)
  - 640 (2 s.f.)
- Zeros after non-zero digits within a number with decimals are significant
  - 689.0023 (7 s.f.)
- Zeros after a decimal point are also significant
  - 70.0 (3 s.f.)
  - 0.0350 (3 s.f.)
When rounding to a certain number of significant figures:
- Identify the significant figures within the number using the rules above
- Count from the first significant figure to the specified number
- Use the next number as the ‘rounder decider’
- If the decider is 5 or greater, increase the previous value by 1
The same approach can be applied to decimal places, although significant figures are more common

Worked Example

Write 1.0478 to 3 significant figures.

Answer:

Step 1: Identify the significant figures

There are 5 significant figures in the number 1.0478 as all the digits are significant

Step 2: Count to the specified number

The question says to 3 significant figures, so the fourth digit is the 'rounder decider'
1.0478

Step 3: Round the final answer up to 3 significant figures

1.05 (3 s.f.)

An appropriate number of significant figures

The appropriate number of significant figures depends on:
- the precision of the measurement
- the limitations of the equipment used to make the measurement
When performing calculations involving measured values, it's essential to maintain the proper number of significant figures throughout the calculation to avoid rounding errors
- It is recommended to use at least two additional significant figures during the working out
- Only round the final answer to the number of significant figures required
In the final result, the number of significant figures should not exceed the value with the least number of significant figures used in the calculation
- The value with the least number of significant figures is the least precise value
- Therefore, the answer obtained from the calculation can only be as precise as this least precise value

Worked Example

The density of gold is 1.93 × 10⁴ kg m^-3.

Calculate the mass of a gold bar of length 49.96 mm, width 29.96 mm, and height 1.6 mm. Give your answer to an appropriate number of significant figures.

Answer:

Step 1: Convert the lengths into metres

1 mm = 1 × 10^-3 m
Length, $l$ = 49.96 mm = 49.96 × 10^-3 m
Width, $w$ = 29.96 mm = 29.96 × 10^-3 m
Height, $h$ = 1.6 mm = 1.6 × 10^-3 m

Step 2: Calculate the volume of the gold bar

$V = l \times w \times h$

$V = (49.96 \times 10^{- 3}) \times (29.96 \times 10^{- 3}) \times (1.6 \times 10^{- 3})$

$V$ = 2.392 × 10^-6 m³

Step 3: Calculate the mass of the gold bar

$m = ρ V$

$m = (1.93 \times 10^{4}) \times (2.392 \times 10^{- 6})$

$m$ = 0.04617 kg

Step 4: Give the answer to the appropriate number of significant figures

The density is given to 3 significant figures
The length and width are given to 4 significant figures
The height is given to 2 significant figures
- Therefore, the appropriate number of significant figures is 2
So, the final answer is 0.046 kg

Examiner Tips and Tricks

Exam questions sometimes ask you to give an answer to:
- a certain number of significant figures, usually 2 or 3
- an appropriate number of significant figures
Make sure you keep an eye out for this, as it can be an easy and frustrating mark to lose after all your hard work in the calculation

For constants, such as the acceleration of free fall or the speed of light, the number of significant figures is not limited by measurement precision but rather by the definition of the constant itself
In these cases, use the defined number of significant figures provided for that constant, e.g. in the data booklet:
- the acceleration of free fall $g$ (9.8 m s^-1) is given to 2 significant figures
- the speed of light $c$ (3.00 × 10⁸ m s^-1) is given to 3 significant figures

Orders of magnitude

When a number is expressed to an order of 10, this is an order of magnitude
- For example, the order of magnitude of 3 × 10⁸ is 10⁸
Orders of magnitude follow rules for rounding
- The order of magnitude of 6 × 10⁸ is 10⁹, as the magnitude is rounded up
A quantity is one order of magnitude larger than another quantity if it is about ten times larger
- Similarly, two orders of magnitude would be 100 times larger, or 10²
In physics, it can be difficult to comprehend the size of quantities that are very large or very small
Expressing a quantity as an order of magnitude makes it easier to compare it with more familiar quantities
- For example, the length of a football field is about 100 m, or ~ 10² m
- The distance between the Earth and the Sun is 1.5 × 10¹¹ m, or ~ 10¹¹ m
- The difference is $\frac{10^{11}}{10^{2}}$ = 10⁹, or 9 orders of magnitude, which means 10⁹ (a billion) football fields could fit between the Earth and the Sun

Comparison of distances

Quantity	Length / m	Order of magnitude / m
distance to the edge of the observable Universe	4.40 × 10²⁶	10²⁶
distance from Earth to Neptune	4.5 × 10¹²	10¹²
distance from London to Cape Town	9.7 × 10⁶	10⁷
length of a human	1.7	10⁰
length of an ant	9 × 10⁻⁴	10⁻³
length of a bacteria cell	2 × 10⁻⁶	10⁻⁶

Approximation and estimation

Approximation is about simplifying a calculation or model to obtain a value that is close to the actual value, but not exact
Typically used when a precise calculation is unnecessary or not possible
Use approximation to
- simplify equations
- neglect small effects, e.g. air resistance
- apply specific rules, e.g. the small-angle approximation

Estimation is about making a reasoned guess based on available data
Typically used when the true value is unknown or can't be directly measured
Use estimation to
- carry out quick order of magnitude calculations
- make an educated guess based on incomplete information
- check if a result is reasonable

Worked Example

Estimate the order of magnitude of the following:

(a) The temperature of an oven (in Kelvin)

(b) The volume of the Earth (in m³)

Answer:

(a) Estimate the temperature of an oven

A conventional oven works at ∼200 °C
T (in K) = 200 + 273 = 473 K
This is equivalent to 4.73 × 10² K
The order of magnitude is ∼10² K

(b) Estimate the volume of the Earth

The radius of the Earth is ∼6.4 × 10⁶ m
The volume of a sphere is equal to:
- $V = \frac{4}{3} π r^{3}$
- $V = \frac{4}{3} π \times {(6.4 \times 10^{6})}^{3}$ = 1.1 × 10²¹ m³
The order of magnitude is ∼10²¹ m³

(c) Estimate the number of seconds in 95 years

1 year = 365 × 24 × 60 × 60 = 31 536 000 s
95 years = 95 × 31 536 000 = 283 824 000 s
This is approximately 2.84 × 10⁸ s
Therefore, the order of magnitude is ∼10⁸ s

Appreciate when some effects can be ignored and why this is useful

In physics, we often make assumptions to simplify problems
A common assumption is to ignore effects which are considered negligible
- This means its influence on the system is so small that it has no significant effect on the outcome of the results
Examples of negligible effects
- Air resistance
  - depends on the shape of the object and the speed at which it is travelling
  - can be ignored for small objects (e.g. a ball) moving over short distances at low speeds
  - cannot be ignored for large objects (e.g. a parachute) moving over long distances at high speeds
- Friction
  - depends on the roughness of the surface
  - can be ignored when the surface is described as 'smooth'
  - cannot be ignored when an object slows down or loses energy as it moves over a surface
- Thermal losses
  - can be ignored when the heat lost to the surroundings is much smaller than the energy transfers within the system
  - e.g. specific heat capacity calculations
- Internal resistance
  - can be ignored when the internal resistance of the supply is much smaller than the load resistance
  - e.g. circuits with low-voltage cells
- Mass
  - can be ignored when the mass of an object has no noticeable effect on a system
  - e.g. in a simple pendulum, the mass of the string can be considered negligible compared to the mass of the bob

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Did this page help you?

Previous:Applying Technology to Process Data in PhysicsNext:Scalar & Vector Quantities

Applying General Mathematics in Physics (DP IB Physics): Revision Note

Algebra & mathematical relationships

Using arithmetic and algebraic calculations in physics

Areas and volumes

Decimals, fractions, percentages and ratios

Reciprocals and exponents

Trigonometric ratios

Logarithmic and exponential functions

Determine rates of change

Calculate the mean and range

Mean

Range

Equations and derivations in physics

Select and manipulate equations

Derive relationships algebraically

Continuous and discrete variables

Direct and inverse proportionality

Determine the effect of changing variables

Percentage change and percentage difference

Percentage change

Percentage difference

Percentage error

Percentage uncertainty

Scientific notation & significant figures

What is scientific notation?

Applying scientific notation to numbers

Significant figures

An appropriate number of significant figures

Orders of magnitude

Comparison of distances

Approximation and estimation

Appreciate when some effects can be ignored and why this is useful

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Space, Time & Motion

Kinematics

Distance & Displacement

Speed & Velocity

Acceleration

Kinematic Equations

Motion Graphs

Projectile Motion

Fluid Resistance

Terminal Speed

Forces & Momentum

Free-Body Diagrams

Newton’s First Law

Newton’s Second Law

Newton’s Third Law

Contact Forces

Non-Contact Forces

Frictional Forces

Hooke's Law

Stoke's Law

Buoyancy

Conservation of Linear Momentum

Impulse & Momentum

Force & Momentum

Collisions & Explosions in One-Dimension

Collisions & Explosions in Two-Dimensions

Angular Velocity

Centripetal Force

Centripetal Acceleration

Non-Uniform Circular Motion

Work, Energy & Power

Principle of Conservation of Energy

Sankey Diagrams

Work Done

Kinetic Energy

Gravitational Potential Energy

Elastic Potential Energy

Conservation of Mechanical Energy

Energy & Power

Efficiency Formula

Energy Density

Rigid Body Mechanics

Torque & Couples

Rotational Equilibrium

Angular Displacement, Velocity & Acceleration

Angular Acceleration Formula