Arc Lengths & Sector Areas (Edexcel IGCSE Maths A): Revision Note
Exam code: 4MA1
Did this video help you?
Arc lengths & sector areas
What is an arc?
An arc is a part of the circumference of a circle
Two points on a circumference of a circle will create two arcs
The smaller arc is known as the minor arc
The bigger arc is known as the major arc
What is a sector?
A sector is the part of a circle enclosed by two radii (radiuses) and an arc
A sector looks like a slice of a circular pizza
The curved edge of a sector is the arc
Two radii in a circle will create two sectors
The smaller sector is known as the minor sector
The bigger sector is known as the major sector
What formulae do I need to know?
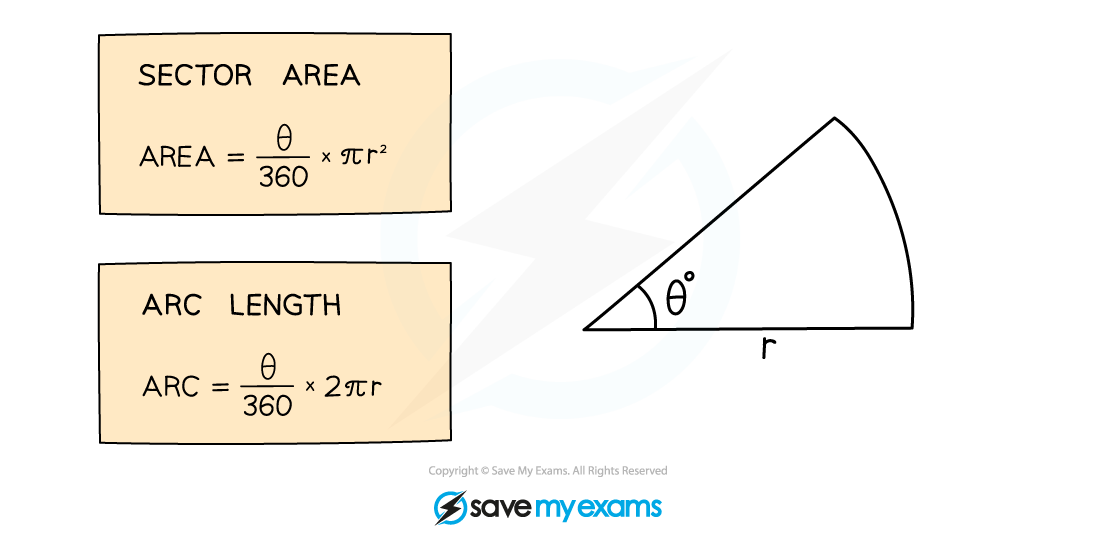
You need to be able to calculate the length of an arc and the area of a sector
The angle formed in a sector by the two radii is often labelled θ (the Greek letter “theta”)
You can calculate the area of a sector or the length of an arc by adapting the formulae for the area or circumference of a circle
A full circle is equal to 360° so the fraction will be the angle, θ°, out of 360°
Working with sector and arc formulae is just like working with any other formula:
Write down what you know (or what you want to know)
Pick the correct formula
Substitute the values in and solve
How do I find the length of an arc?
STEP 1
Divide the angle by 360 to form a fractionSTEP 2
Calculate the circumference of the full circleSTEP 3
Multiply the fraction by the circumference
How do I find the area of a sector?
STEP 1
Divide the angle by 360 to form a fractionSTEP 2
Calculate the area of the full circleSTEP 3
Multiply the fraction by the area
Examiner Tips and Tricks
Make sure you remember the formulas for the circumference and area of a circle, as they are not given in the exam.
Arc length and sector area are then just a fraction of these formulas.
Worked Example
A sector of a circle is shown.
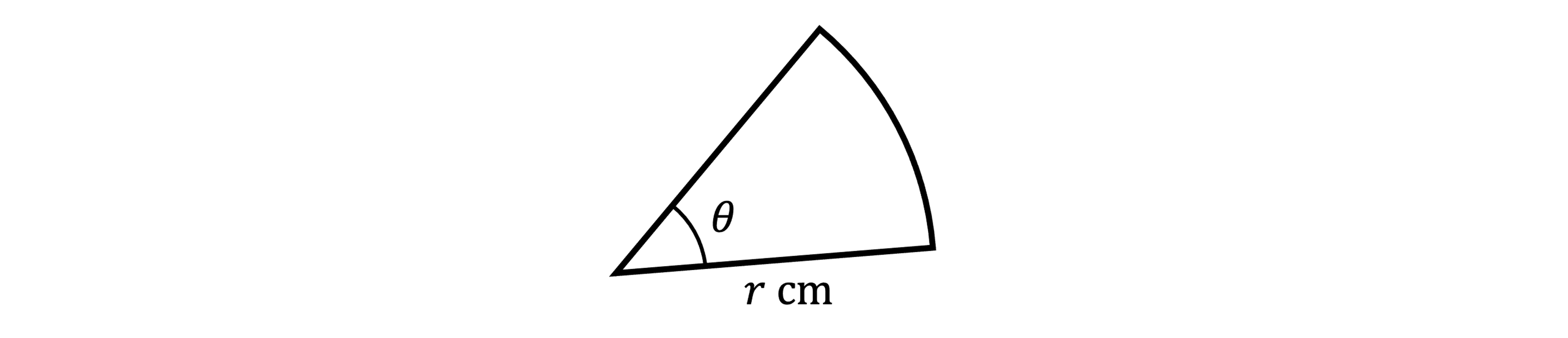
The angle, θ, is 72° and the radius, r, is 5 cm.
(a) Find the area of the sector, giving your answer correct to 3 significant figures.
Answer:
Substitute θ = 72° and r = 5 into the formula for the area of a sector,
Use a calculator to work out this value
15.70796...
Round your answer to 3 significant figures
15.7 cm2
(b) Find the length of the arc of the sector, giving your answer as a multiple of .
Answer:
Substitute θ = 72° and r = 5 into the formula for the length of an arc,
Simplify the number part without
Write down the final answer with
2π cm

Unlock more, it's free!
Did this page help you?