Revision NotesExam QuestionsFlashcardsPast PapersMock Exams
IBMathsDPAnalysis & Approaches (AA)HLRevision Notes3. Geometry & TrigonometryVector PropertiesParallel Vectors

Parallel Vectors (DP IB Analysis & Approaches (AA)): Revision Note

Amber

Author

Amber

Last updated

DP Analysis & Approaches (AA): HLDP Applications & Interpretation (AI): HLDP Applications & Interpretation (AI): HLDP Analysis & Approaches (AA): HL

Did this video help you?

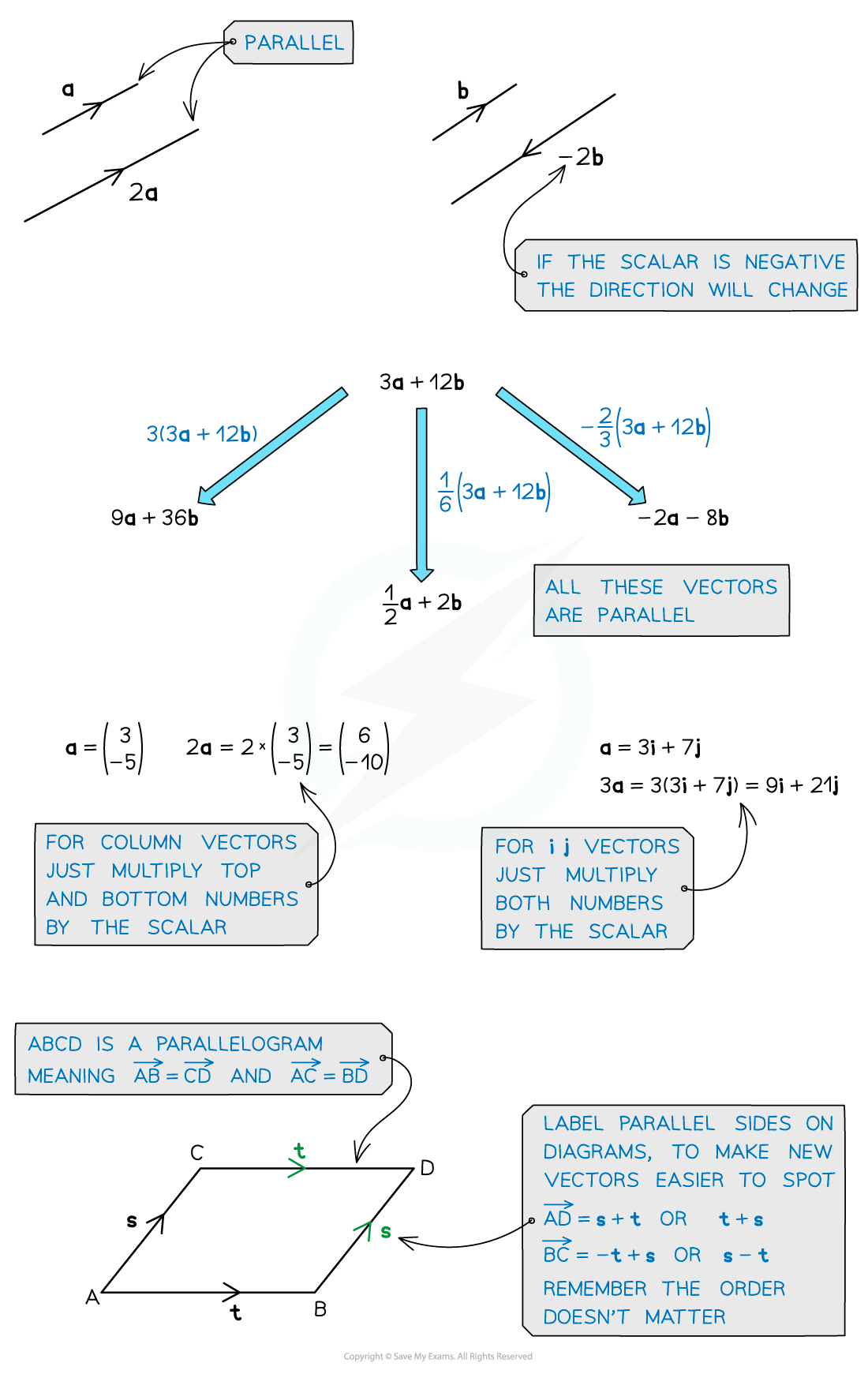
Parallel Vectors

How do you know if two vectors are parallel?

  • Two vectors are parallel if one is a scalar multiple of the other

    • This means that all components of the vector have been multiplied by a common constant (scalar)

  • Multiplying every component in a vector by a scalar will change the magnitude of the vector but not the direction

    • For example: the vectors begin mathsize 16px style bold a equals blank open parentheses fraction numerator 1 over denominator table row 0 row 3 end table end fraction close parentheses end style and begin mathsize 16px style bold b equals 2 bold a equals blank 2 open parentheses fraction numerator 1 over denominator table row 0 row 3 end table end fraction close parentheses equals blank open parentheses fraction numerator 2 over denominator table row 0 row 6 end table end fraction close parentheses end style will have the same direction but the vector b will have twice the magnitude of a

      • They are parallel

  • If a vector can be factorised by a scalar then it is parallel to any scalar multiple of the factorised vector

    • For example: The vector 9i + 6j – 3k can be factorised by the scalar 3 to 3(3i + 2j – k) so the vector 9i + 6j – 3k is parallel to any scalar multiple of 3i + 2j – k

  • If a vector is multiplied by a negative scalar its direction will be reversed

    • It will still be parallel to the original vector

  • Two vectors are parallel if they have the same or reverse direction and equal if they have the same size and direction

Vector Addition Diagram 2

Examiner Tips and Tricks

  • It is easiest to spot that two vectors are parallel when they are in column vector notation

    • in your exam by writing vectors in column vector form and looking for a scalar multiple you will be able to quickly determine whether they are parallel or not

Worked Example

Show that the vectors bold a space equals space open parentheses fraction numerator table row 2 row 0 end table over denominator negative 4 end fraction close parentheses and bold b space equals space 6 bold k space – space 3 bold i are parallel and find the scalar multiple that maps a onto b.

3-9-2-ib-aa-hl-parallel-vectors-we-solution

You've read 0 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Introduction to VectorsNext:Adding & Subtracting Vectors
    Amber

    Author: Amber

    Expertise: Maths Content Creator

    Amber gained a first class degree in Mathematics & Meteorology from the University of Reading before training to become a teacher. She is passionate about teaching, having spent 8 years teaching GCSE and A Level Mathematics both in the UK and internationally. Amber loves creating bright and informative resources to help students reach their potential.