Revision NotesExam QuestionsFlashcardsPast PapersMock Exams
IBMathsDPAnalysis & Approaches (AA)HLRevision Notes3. Geometry & TrigonometryInverse & Reciprocal Trigonometric FunctionsInverse Trigonometric Functions

Inverse Trigonometric Functions (DP IB Analysis & Approaches (AA)): Revision Note

Amber

Written by: Amber

Reviewed by: Dan Finlay

Updated on

Inverse trig functions

What are the inverse trig functions?

  • The inverse trig functions are

    • arcsin x equals sin to the power of negative 1 end exponent x

    • arc cos x equals cos to the power of negative 1 end exponent x

    • arc tan x equals tan to the power of negative 1 end exponent x

  • They are inverses when the domains are restricted

    • arcsin x is the inverse of sin x when its domain is negative straight pi over 2 less or equal than x less or equal than straight pi over 2

      • e.g. sin open parentheses straight pi over 2 close parentheses equals 1 rightwards double arrow arcsin open parentheses 1 close parentheses equals straight pi over 2

    • arc cos x is the inverse of cos x when its domain is 0 less or equal than x less or equal than straight pi

      • e.g. cos open parentheses straight pi over 3 close parentheses equals 1 half rightwards double arrow arc cos open parentheses 1 half close parentheses equals straight pi over 3

    • arc tan x is the inverse of tan x when its domain is negative straight pi over 2 less than x less than straight pi over 2

      • e.g. tan open parentheses straight pi over 4 close parentheses equals 1 rightwards double arrow arc tan open parentheses 1 close parentheses equals straight pi over 4

Examiner Tips and Tricks

Be careful when you are working outside these domains. For example, sin open parentheses 2 straight pi close parentheses equals 1 but arcsin open parentheses 1 close parentheses not equal to 2 straight pi.

What do the graphs of the inverse trig functions look like?

y=arcsinx

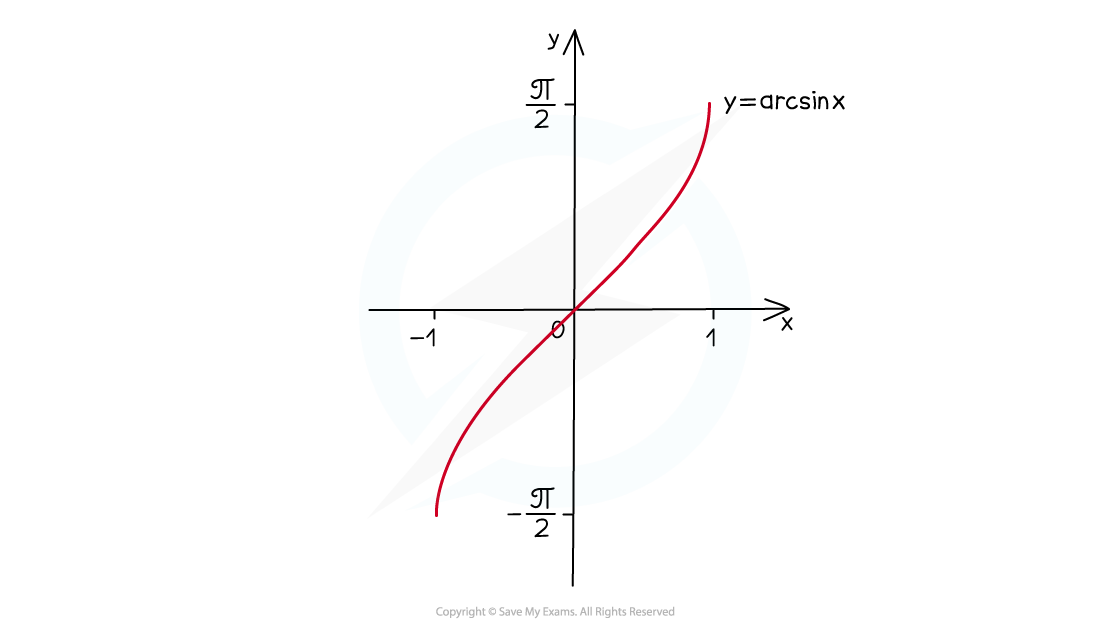
  • y equals arcsin x is a reflection of y equals sin x in the line y equals x when its domain is negative straight pi over 2 less or equal than x less or equal than straight pi over 2

  • The domain is negative 1 space less or equal than space x space less or equal than space 1

  • The range is negative pi over 2 less or equal than space y space less or equal than pi over 2

Graph of the arcsine function, y = arcsin(x), with a curved red line. X-axis from -1 to 1, y-axis from -π/2 to π/2, passing through origin.
The graph of y=arcsinx

y=arccosx

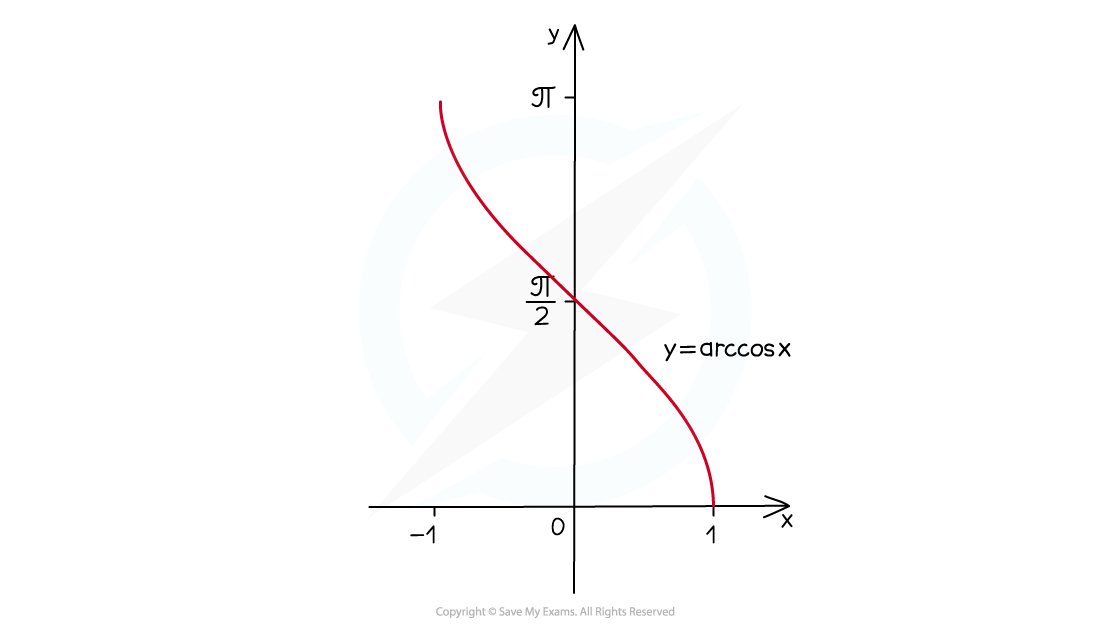
  • y equals arc cos x is a reflection of y equals cos x in the line y equals x when its domain is 0 less or equal than x less or equal than straight pi

  • The domain is negative 1 space less or equal than space x space less or equal than space 1

  • The range is 0 less or equal than space y space less or equal than pi

Graph of y = arccos(x) in red, spanning x-axis from -1 to 1 and y-axis from 0 to π, with marked π/2 point.
The graph of y=arccosx

y=arctanx

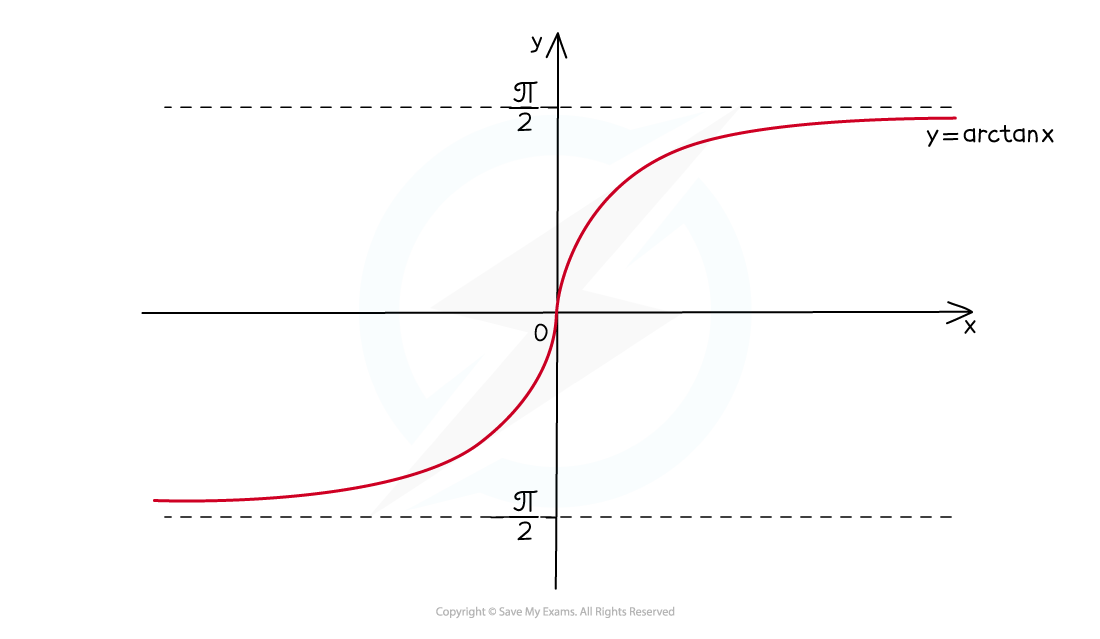
  • y equals arc tan x is a reflection of y equals tan x in the line y equals x when its domain is negative straight pi over 2 less than x less than straight pi over 2

  • The domain is x element of straight real numbers

  • The range is negative pi over 2 less than space y space less than pi over 2

  • There are horizontal asymptotes at y equals plus-or-minus straight pi over 2

Graph of y = arctan(x) with a red curve. Asymptotes at y = π/2 and y = -π/2. The curve crosses the origin, approaching horizontal lines.
The graph of y=arctanx

How can I use inverse trig functions?

  • You can use the inverse trig functions to help you to solve trig equations

    • e.g. if sin x equals 1 third then one solution is x equals arcsin open parentheses 1 third close parentheses

    • You need to use the symmetries of the trig functions to find the other solutions

  • You can solve equations involving inverse trig equations

    • arcsin x equals k rightwards double arrow x equals sin k

    • The converse is not always true

    • You need to use the symmetries to make the value in the trig function be within its restricted domain

      • e.g. sin open parentheses fraction numerator 7 straight pi over denominator 8 end fraction close parentheses equals sin open parentheses straight pi over 8 close parentheses

      • Therefore sin open parentheses fraction numerator 7 straight pi over denominator 8 end fraction close parentheses equals x rightwards double arrow arcsin x equals straight pi over 8

Worked Example

Given that xsatisfies the equation arccos blank x blank equals blank k where blank pi over 2 less than k less than pi,  state the range of possible values of x.

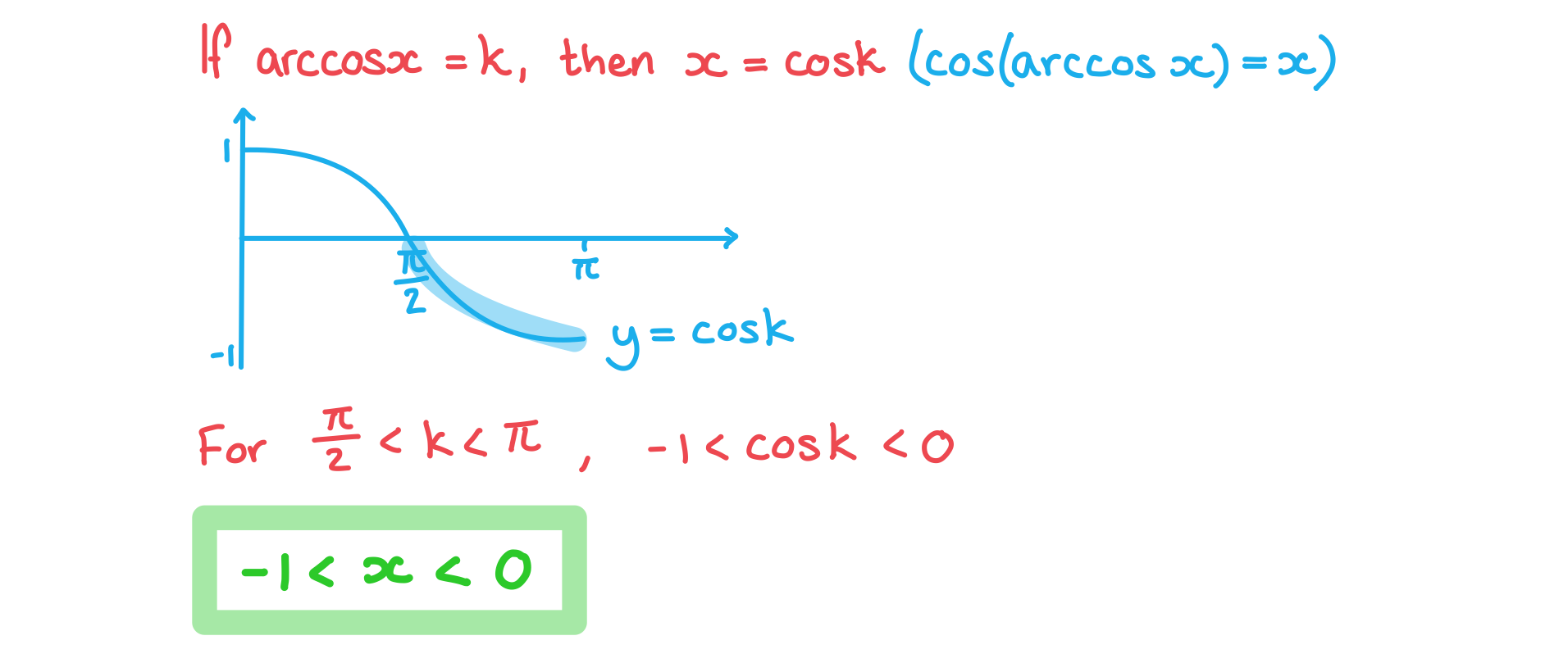
BpKJi_8r_3-7-2-ib-aa-hl-we-solution-inverse-functions

You've read 0 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcards
    Previous:Reciprocal Trigonometric FunctionsNext:Trigonometric Proof
    Author
    Reviewer
    Amber

    Author: Amber

    Expertise: Maths Content Creator

    Amber gained a first class degree in Mathematics & Meteorology from the University of Reading before training to become a teacher. She is passionate about teaching, having spent 8 years teaching GCSE and A Level Mathematics both in the UK and internationally. Amber loves creating bright and informative resources to help students reach their potential.

    Dan Finlay

    Reviewer: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.