Reciprocal Trigonometric Functions (DP IB Analysis & Approaches (AA)): Revision Note

Reciprocal trig functions

What are the reciprocal trigonometric functions?

• There are three reciprocal trig functions correspond to either sin, cos or tan

  • Secant is the reciprocal of the cosine function

    •  

  • Cosecant is the reciprocal of the sine function

    • 

  • Cotangent is the reciprocal of tangent function

    •   

• Another formula for cot is

  • 

  • It is just the reciprocal of the tan formula

What do the graphs of the reciprocal trig functions look like?

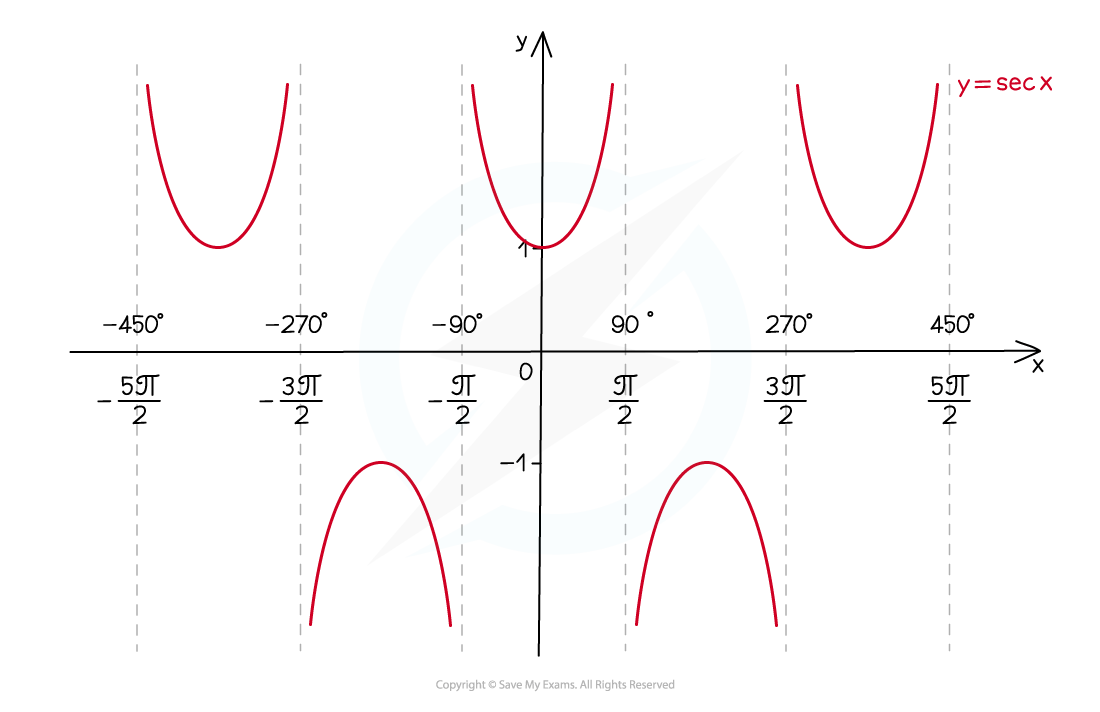
y = secx

• The y-axis is a line of symmetry

• It has a period of 360° (2π radians)

• There are vertical asymptotes wherever

  • If drawing the graph without the help of a GDC it is a good idea to sketch cos x first and draw these in

• The domain is all x except odd multiples of 90° (90°, -90°, 270°, -270°, etc.)

  • in radians this is all x except odd multiples of π/2 (π/2, - π/2, 3π/2, -3π/2, etc.)

• The range is y ≤ -1 or y ≥ 1

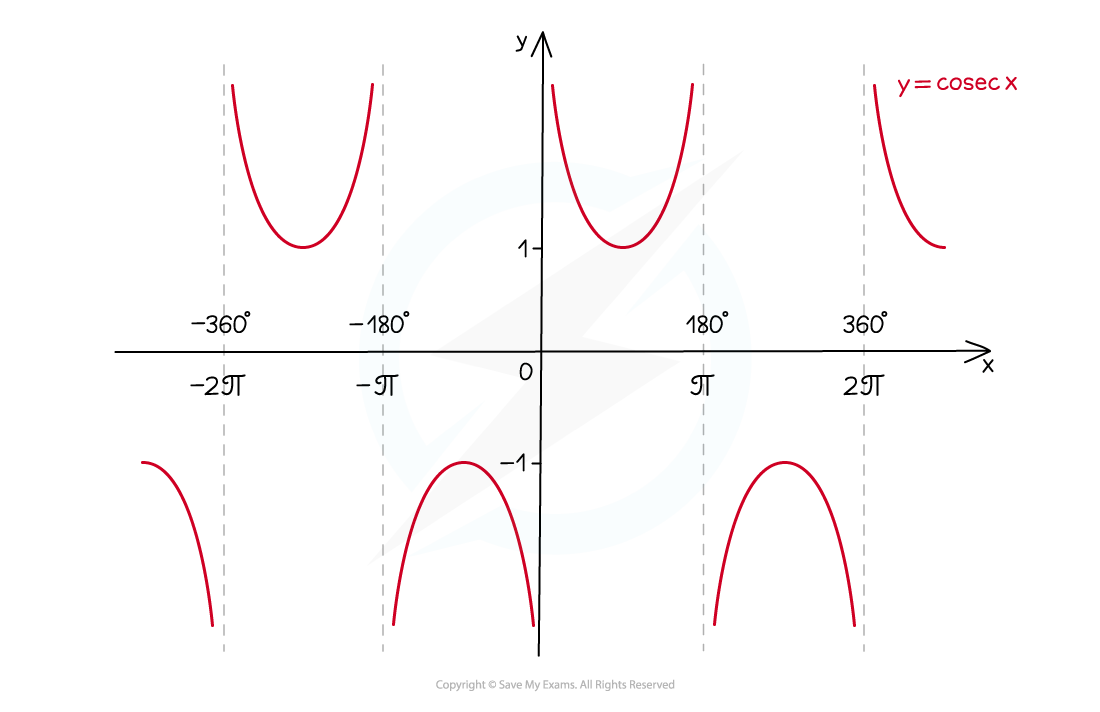
y = cosecx

• It has a period of 360° (2π radians)

• There are vertical asymptotes wherever

  • If drawing the graph it is a good idea to sketch sin x first and draw these in

• The domain is all x except multiples of 180° (0°, 180°, -180°, 360°, -360°, etc.)

  • in radians this is all x except multiples of π (0, π, - π, 2π, -2π, etc.)

• The range is y ≤ -1 or y ≥ 1

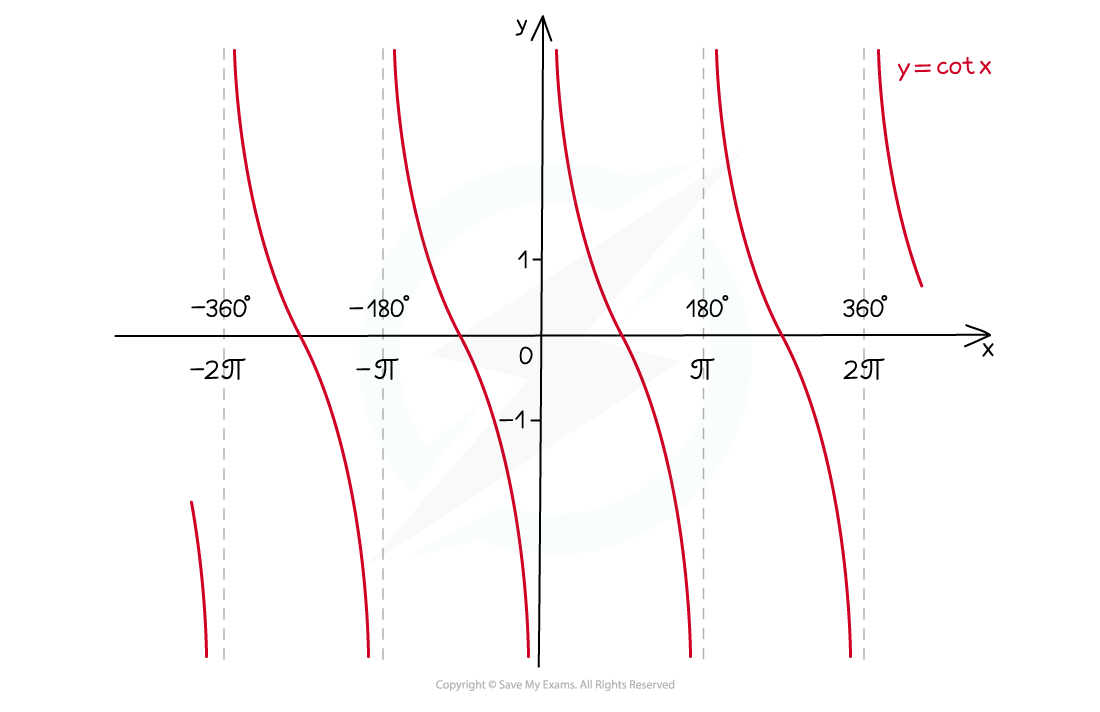
y = cotx

• It has a period of 180° or π radians

• There are vertical asymptotes wherever

• The domain is all x except multiples of 180° (0°, 180°, -180°, 360°, -360°, etc.)

  • In radians this is all x except multiples of π (0, π, - π, 2π, -2π, etc.)

• The range is y ∈ ℝ (i.e. cot can take any real number value)

How do I solve equations using reciprocal trig?

• If there is only one type of reciprocal trig function

  • Isolate it

    • e.g.

  • Take the reciprocal of both sides

    • e.g.

• If there is more than one type of reciprocal trig function

  • Replace the reciprocal trig terms with their identities

    • e.g. can be written as

Pythagorean identities

What are the Pythagorean Identities?

• You know the Pythagorean identity

• There are two further Pythagorean identities

  • 

  • 

How do I derive the Pythagorean Identities?

• You can derive the identities using

  • Dividing all the terms by gives

    • 

  • Dividing all the terms by gives

    • 

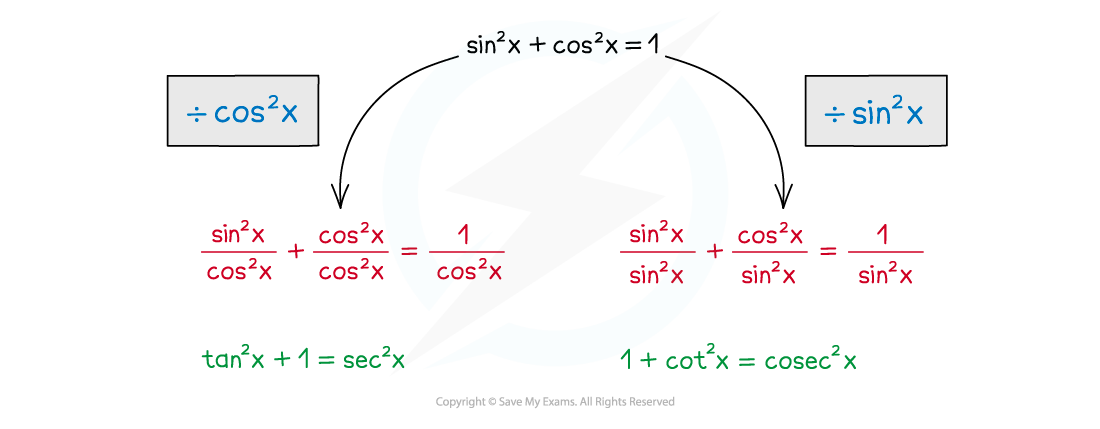
How do I solve equations using the Pythagorean Identities?

• Use the Pythagorean identities if your equation contains either:

  • sec and tan and at least one is squared

  • or cosec and cotan and at least one is squared

• You might need to rearrange the identities

  • 

  •