Adding & Subtracting Vectors (DP IB Analysis & Approaches (AA)): Revision Note

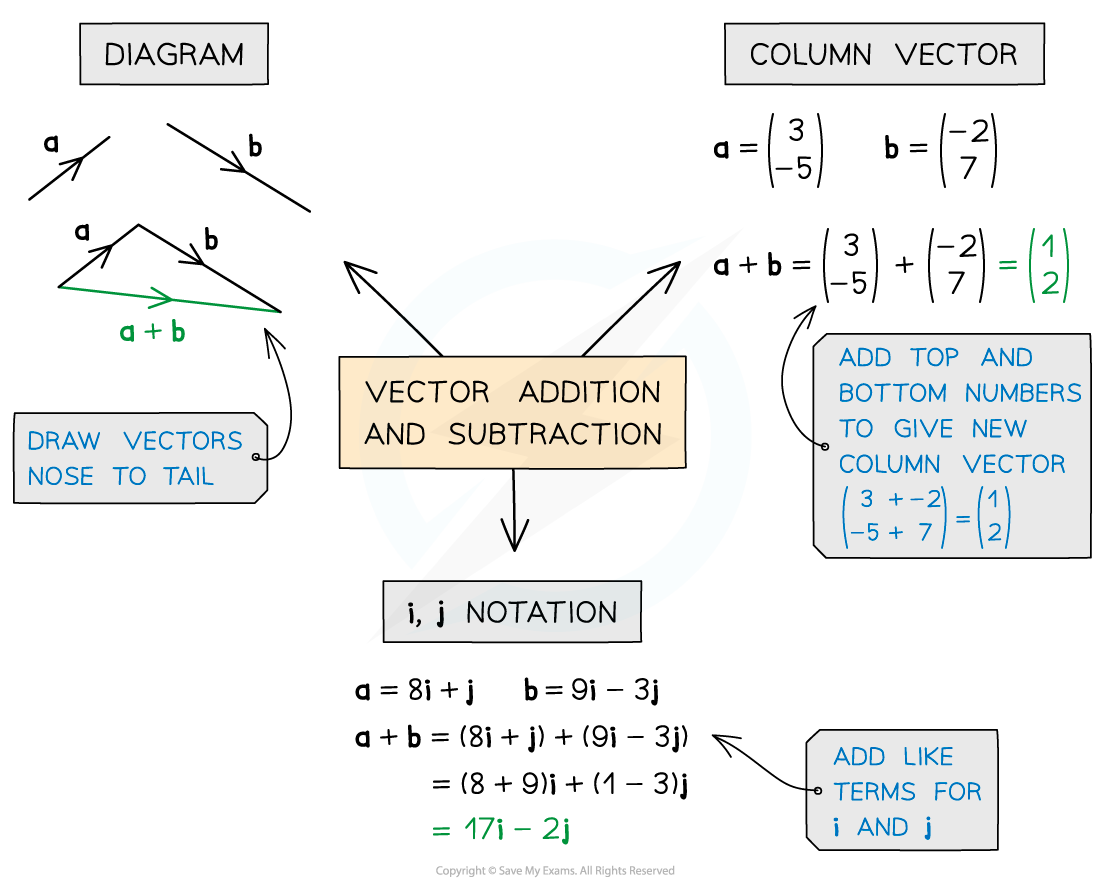
Adding & Subtracting Vectors

How are vectors added and subtracted numerically?

• To add or subtract vectors numerically simply add or subtract each of the corresponding components

• In column vector notation just add the top, middle and bottom parts together

  • For example: 

• In base vector notation add each of the i, j, and k components together separately

  • For example: (2i + j – 5k) – (i + 4j + 3k) = (i – 3j – 8k)
     

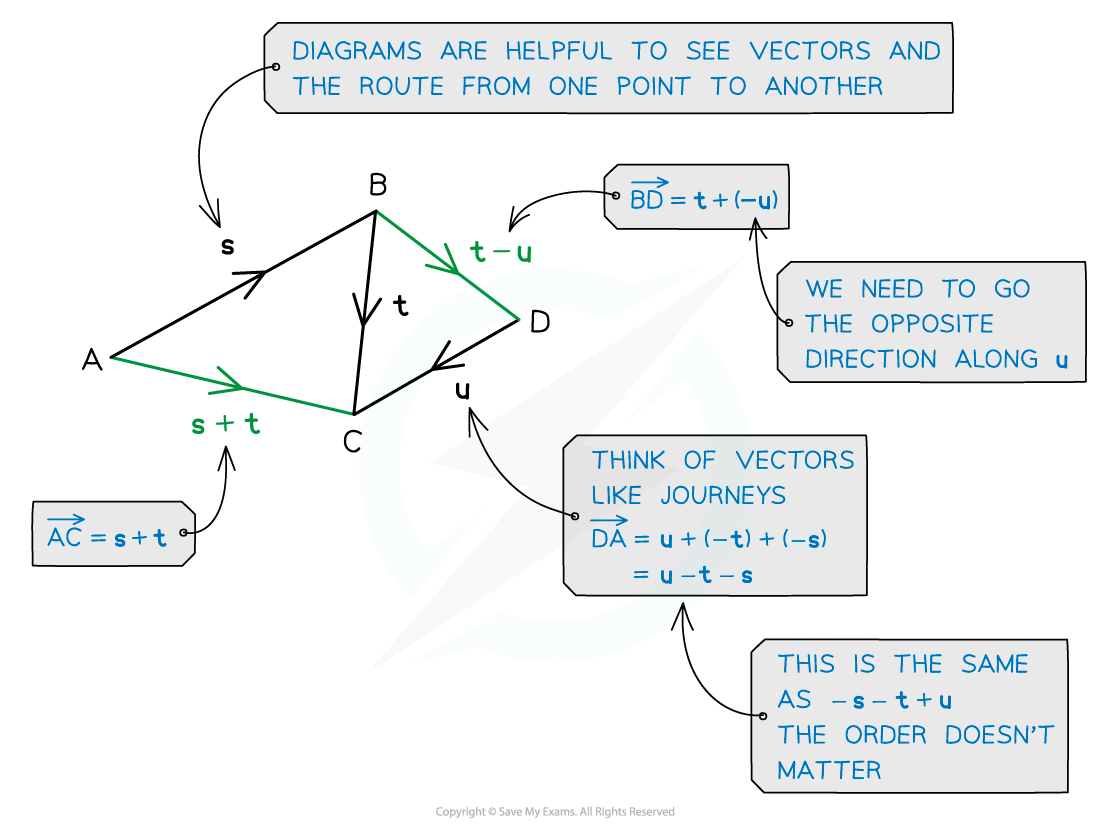
How are vectors added and subtracted geometrically?

• Vectors can be added geometrically by joining the end of one vector to the start of the next one

• The resultant vector will be the shortest route from the start of the first vector to the end of the second

  • A resultant vector is a vector that results from adding or subtracting two or more vectors

• If the two vectors have the same starting position, the second vector can be translated to the end of the first vector to find the resultant vector

  • This results in a parallelogram with the resultant vector as the diagonal

•  To subtract vectors, consider this as adding on the negative vector

  • For example: a – b = a + (-b)

  • The end of the resultant vector a – b will not be anywhere near the end of the vector b

    • Instead, it will be at the point where the end of the vector -b would be