Modulus & Argument (DP IB Analysis & Approaches (AA)): Revision Note
Did this video help you?
Modulus & argument
What is the modulus of a complex number?
The modulus of a complex number (written
or
) is its distance from the origin when plotted on an Argand diagram
If
, then by Pythagoras
A modulus is never negative

In general, adding two complex numbers does not mean you can add their moduli
e.g. both
and
have a modulus of 5
but
has a modulus of 8
How does the modulus relate to the complex conjugate?
The modulus is the result of multiplying a complex number by its conjugate
e.g.
What is the argument of a complex number?
The argument of a complex number (written
or
) is the angle that it makes to the positive real axis on an Argand diagram
measured
counter-clockwise
in radians
where
Arguments are
positive and acute in the first quadrant
positive and obtuse in the second quadrant
negative and obtuse in the third quadrant
negative and acute in the fourth quadrant

Arguments can be calculated using right-angled trigonometry
A sketch is needed to decide the quadrant
positive / negative, or acute / obtuse
then the tan ratio can be used
The argument of zero,
, is undefined
does not exist
as no angle can be drawn
Examiner Tips and Tricks
Occasionally a question may ask for the argument in the range , i.e. all arguments are positive and measured counter-clockwise.
What happens to the modulus and argument under multiplication or division?
When two complex numbers,
and
, are multiplied,
their moduli are also multiplied
but their arguments are added
When two complex numbers,
and
, are divided,
their moduli are also divided
but their arguments are subtracted
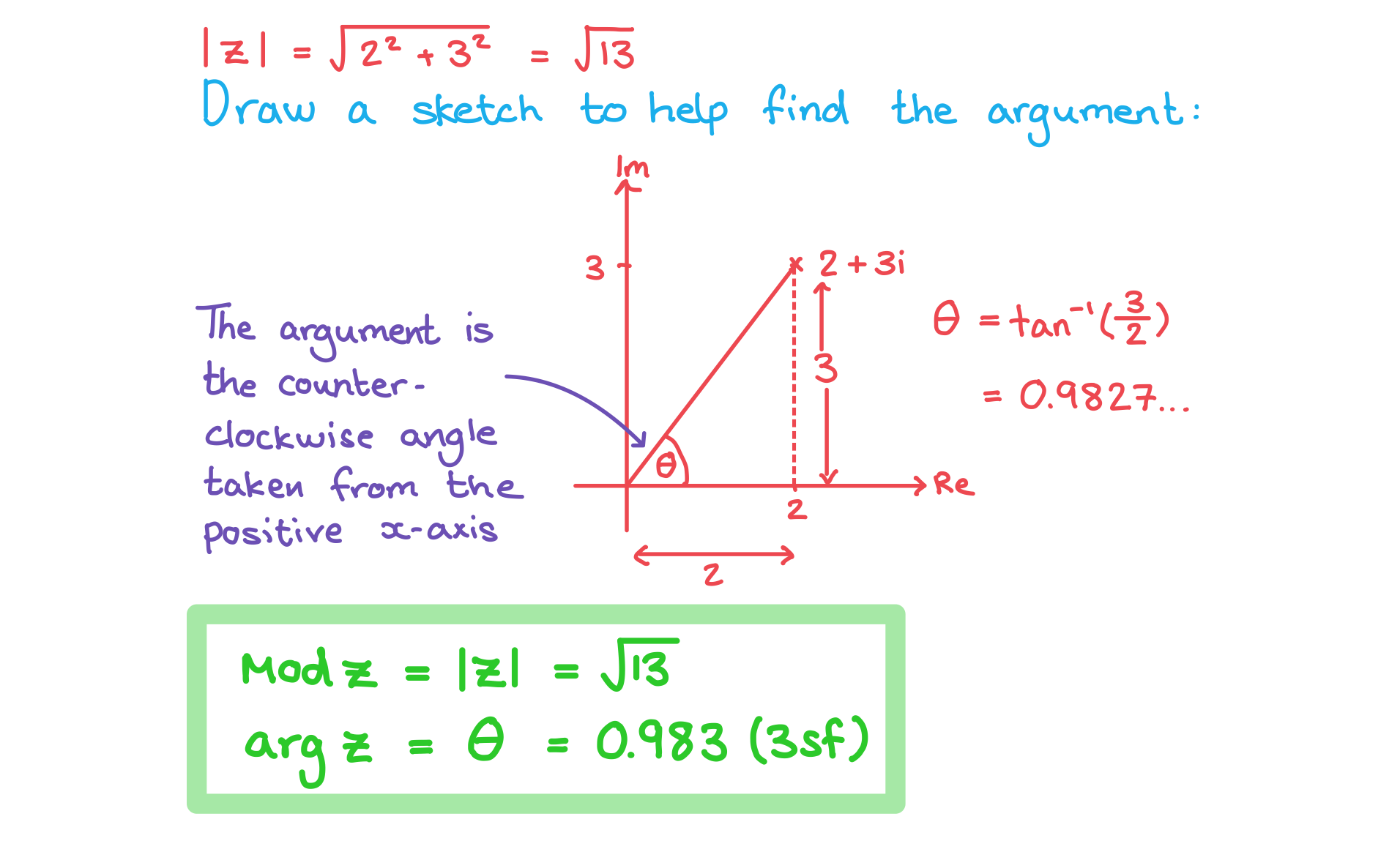
Worked Example
(a) Find the modulus and argument of
Answer:
(b) Find the modulus and argument of
Answer:


Unlock more, it's free!
Did this page help you?