Geometry of Complex Numbers (DP IB Analysis & Approaches (AA)): Revision Note
Did this video help you?
Geometry of complex addition & subtraction
What does addition look like on an Argand diagram?
Addition can be seen using addition of vectors
To add the complex numbers
and
first travel along the vector
then travel along the vector
is the resultant vector
This works in either order
or
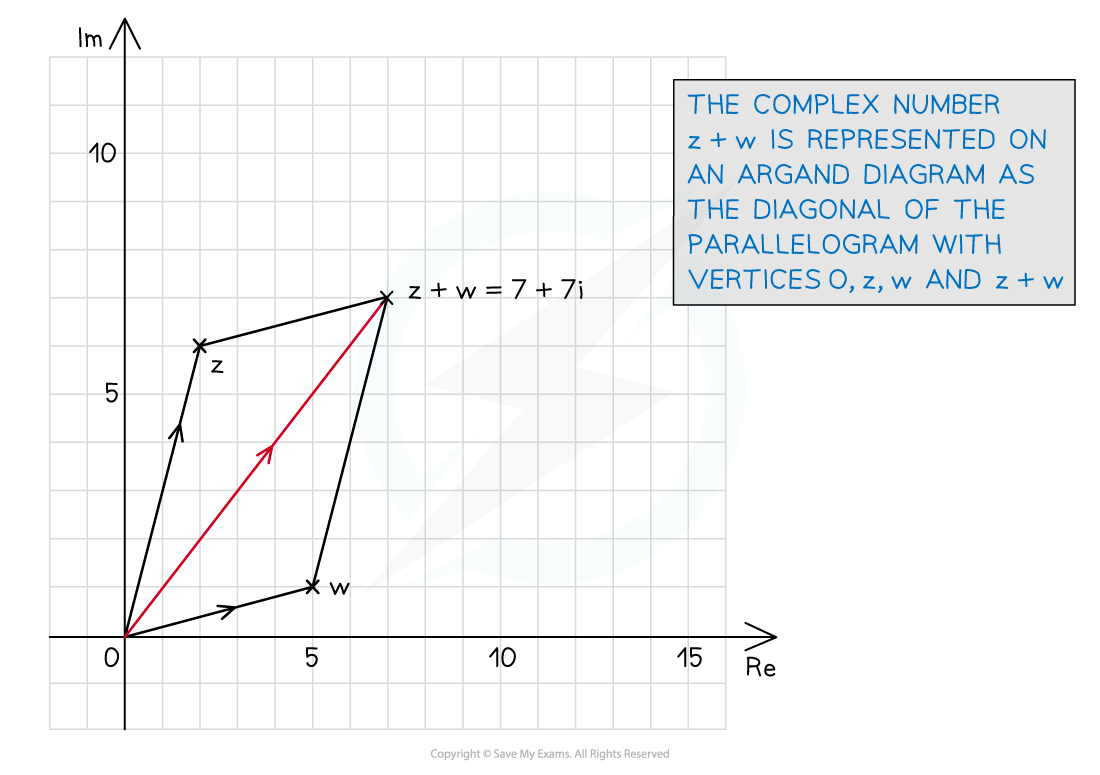
Geometrically, adding
to
is the same as
a translation of
by the vector
What does subtraction look like on an Argand diagram?
Subtraction can be seen using subtraction of vectors
To find
first travel along the vector
then travel along the vector
(the reverse of
)
You cannot swap the order
is not the same as
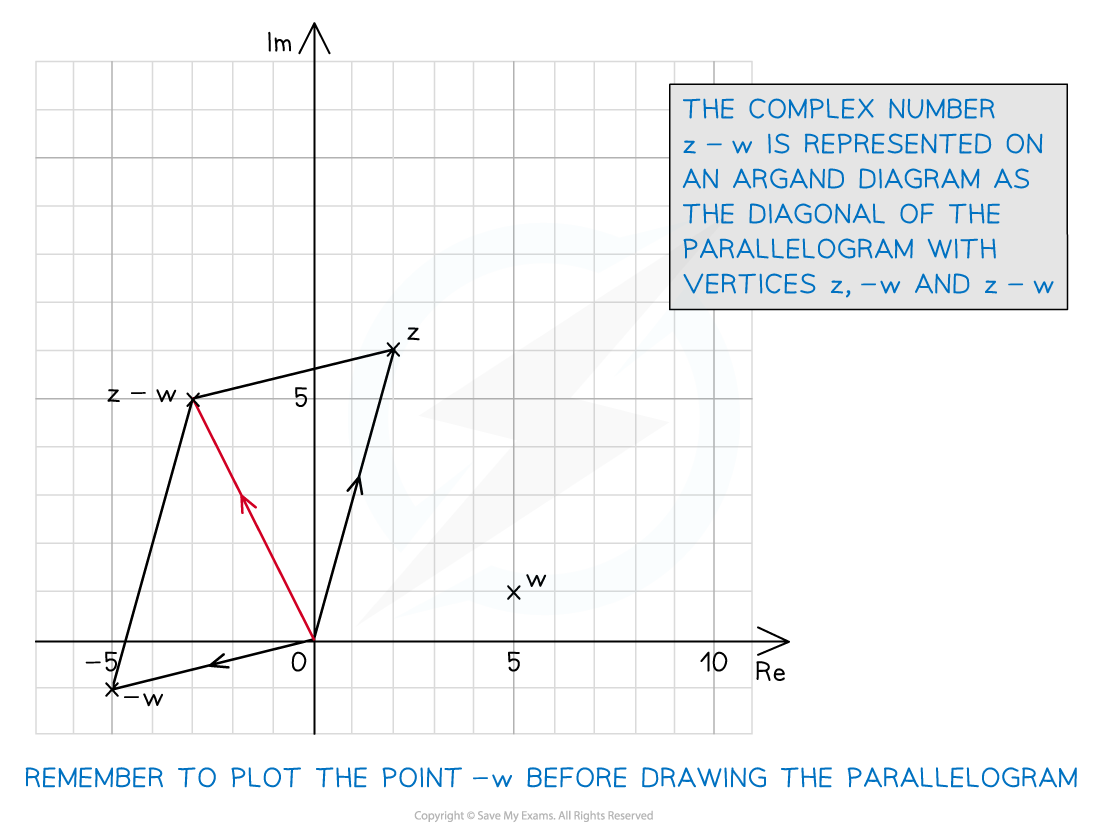
Geometrically, subtracting
from
is the same as
a translation of
by the vector
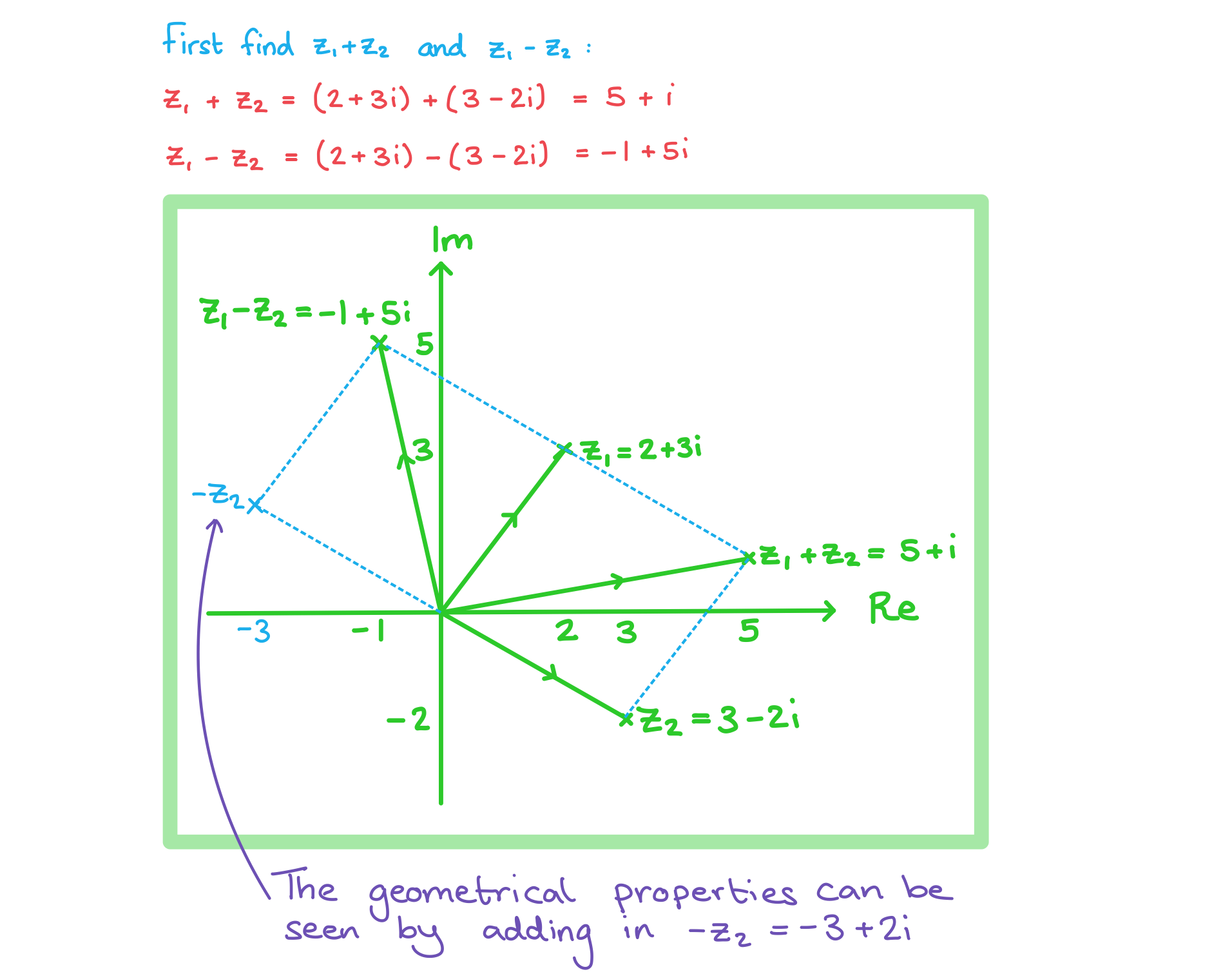
Worked Example
Consider the complex numbers and
.
On an Argand diagram, sketch the complex numbers ,
,
and
.
Answer:
Did this video help you?
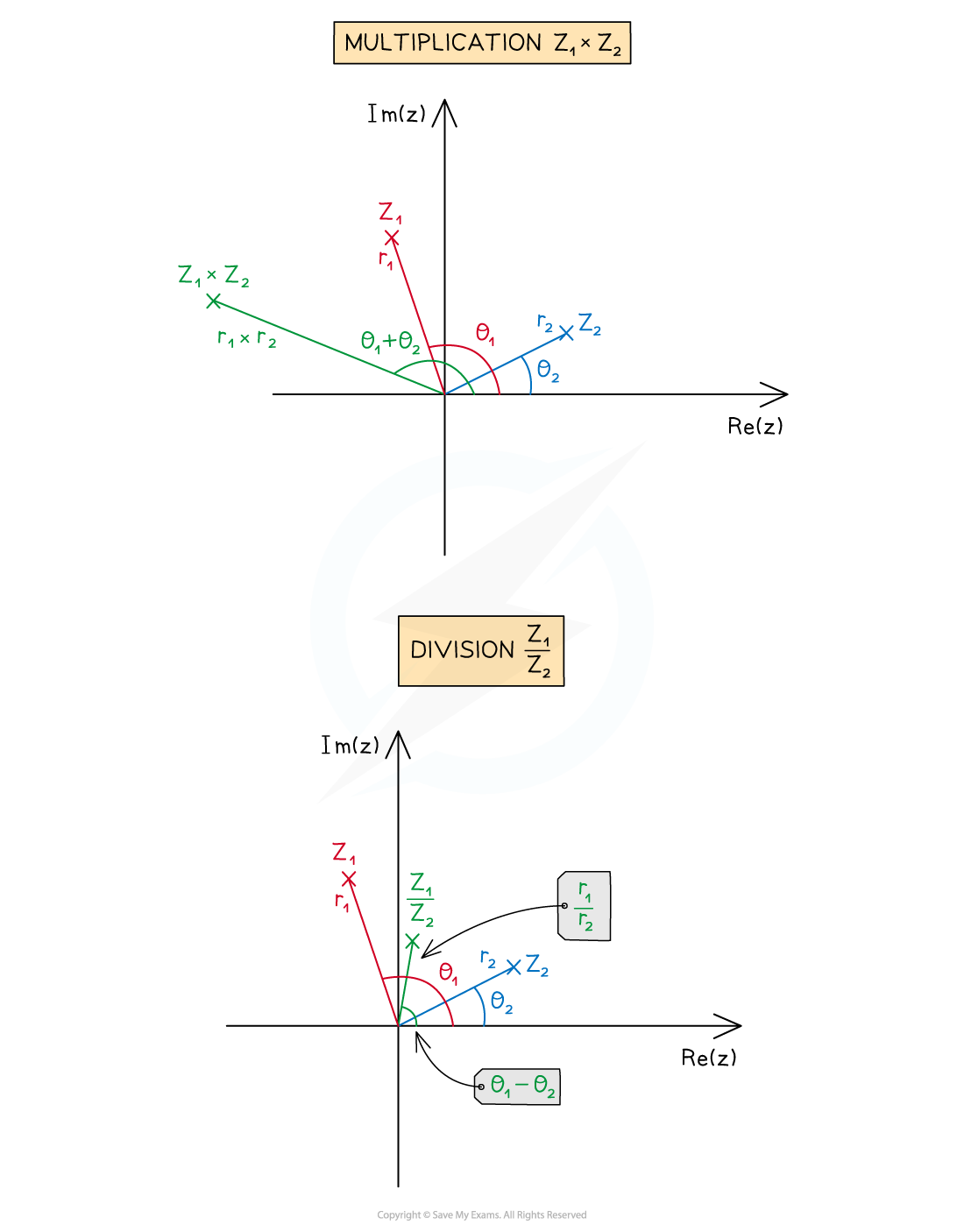
Geometry of complex multiplication & division
What do multiplication and division look like on an Argand diagram?
If the complex number
is multiplied by the complex number
then
will be enlarged by a scale factor of
will be rotated by an angle of
If the complex number
is divided by the complex number
then
will be enlarged by a scale factor of
will be rotated by an angle of
What special cases do I need to know?
Some special cases are
multiplying / dividing
by a real number,
enlarges
by a scale factor of
/
where
could be negative
multiplying / dividing
by an imaginary number,
rotates the point 90° counter-clockwise / clockwise
enlarges
by a scale factor of
/
where
could be negative
What does complex conjugation look like on an Argand diagram?
For the complex number
, the complex conjugate
is a reflection of
in the real axis
Worked Example
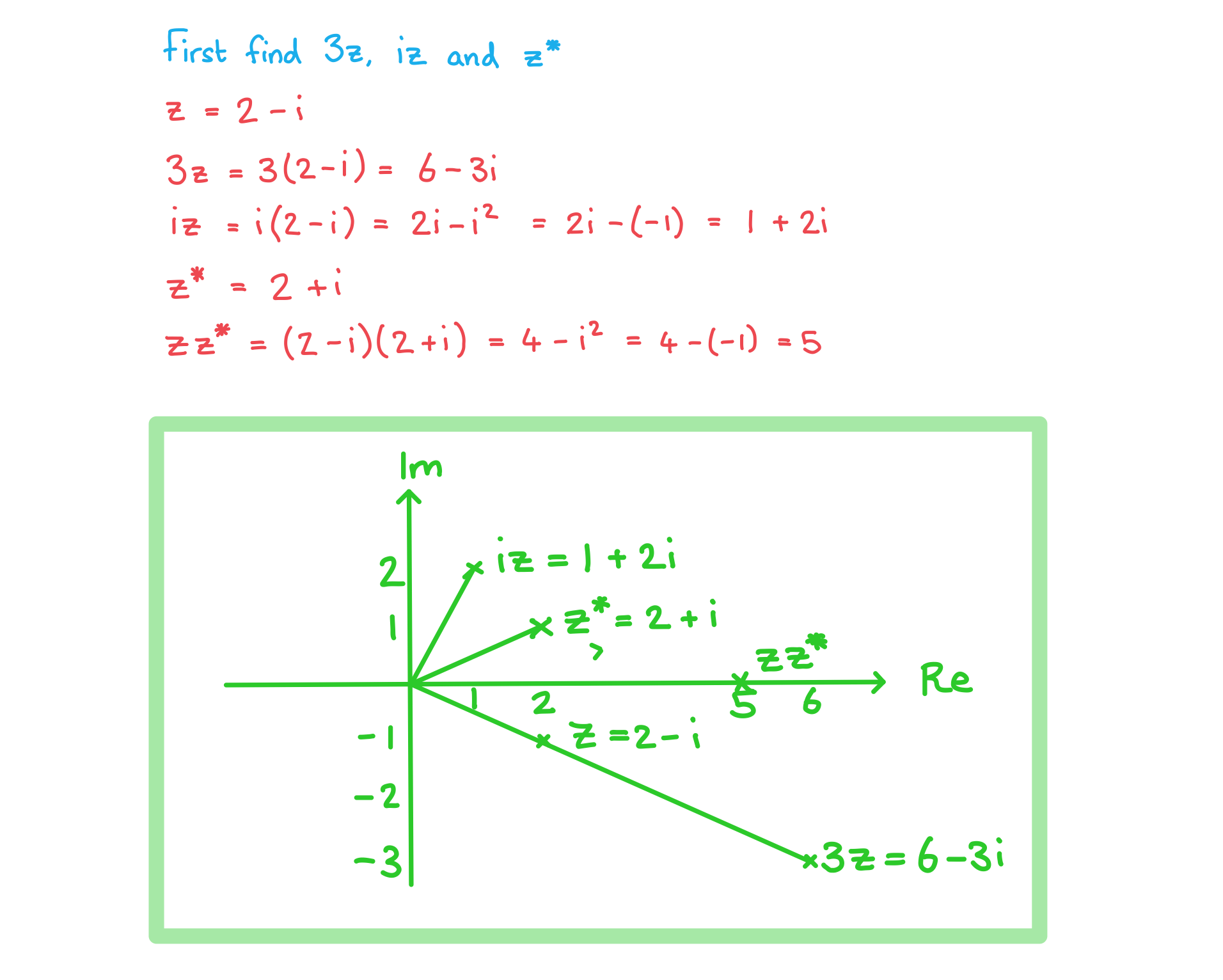
Consider the complex number .
On an Argand diagram, sketch the complex numbers ,
,
,
and
.
Answer:

Unlock more, it's free!
Did this page help you?