Median & Mode of a CRV (DP IB Analysis & Approaches (AA)): Revision Note
Did this video help you?
Median & mode of a CRV
What is meant by the median of a continuous random variable?
The median, m, of a continuous random variable, X, with probability density function f(x) is defined as the value of X such that
Since
this can also be written as
If the p.d.f. is symmetrical (i.e. if the graph of y = f(x) is symmetrical) then the median will be equal to the x-coordinate of the line of symmetry
In such cases the graph of y = f(x) has an axis of symmetry in the line x = m
How do I find the median of a continuous random variable?
The median, m, of a continuous random variable, X, with probability density function f(x) is defined as the value such that
or
The equation that should be used will depend on the information in the question
If the graph of y = f(x) is symmetrical, symmetry may be used to deduce the median
This may often be the case if f(x) is linear and the area under the graph is a basic shape such as a rectangle
How do I find the median of a continuous random variable with a piecewise p.d.f.?
For piecewise functions, the location of the median will determine which equation to use in order to find it
For example
If
then
so the median must lie in the interval 2 ≤ x ≤ 5
So to find the median, m, solve
Because '0.4 of the area' already used for 0 ≤ x ≤ 2
Examiner Tips and Tricks
On a calculator paper, your GDC may be able to solve an equation like directly to find the value of
.
On a non-calculator paper you will need to evaluate such definite integrals in terms of and solve manually,
What is meant by the mode of a continuous random variable?
The mode of a continuous random variable, X, with probability density function f(x) is the value of x that produces the greatest value of f(x)
How do I find the mode of a continuous random variable?
This will depend on the type of function f(x)
The easiest way to find the mode is by considering the shape of the graph of y = f(x)
If the graph is a curve with a maximum point, the mode can be found by differentiating and solving f’(x) = 0
If there is more than one solution to f’(x) = 0 then further work may be needed to deduce the mode
There could be more than one mode
Only consider valid values of x from the domain of the p.d.f.
Use the second derivative (f’’(x)) to deduce the nature of each stationary point
Also check the values of f(x) at the lower and upper limits of x in the domain
One of these could be the maximum value f(x) reaches
Worked Example
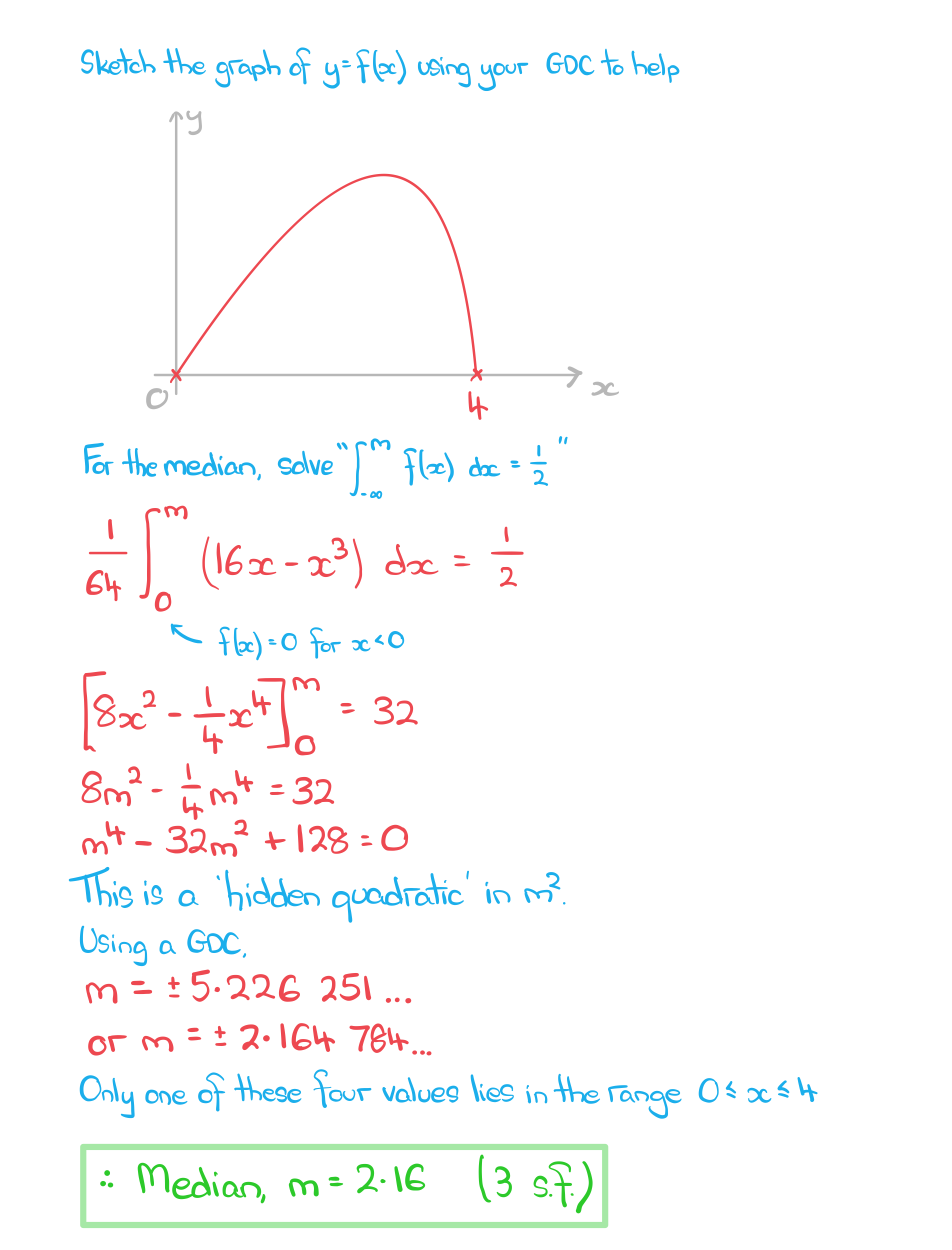
The continuous random variable X has probability function f(x) defined as
a) Find the median of X, giving your answer to three significant figures.
Answer:
b) Find the exact value of the mode of X.
Answer:


Unlock more, it's free!
Was this revision note helpful?
