Revision NotesExam QuestionsFlashcards
IBMaths: AA SLDPRevision Notes4. Statistics & Probability4.3 Probability4.3.3 Sample Space Diagrams

Sample Space Diagrams (DP IB Maths: AA SL)

Revision Note

Dan

Author

Dan

Last updated

Did this video help you?

Venn Diagrams

What is a Venn diagram?

  • A Venn diagram is a way to illustrate events from an experiment and are particularly useful when there is an overlap between possible outcomes
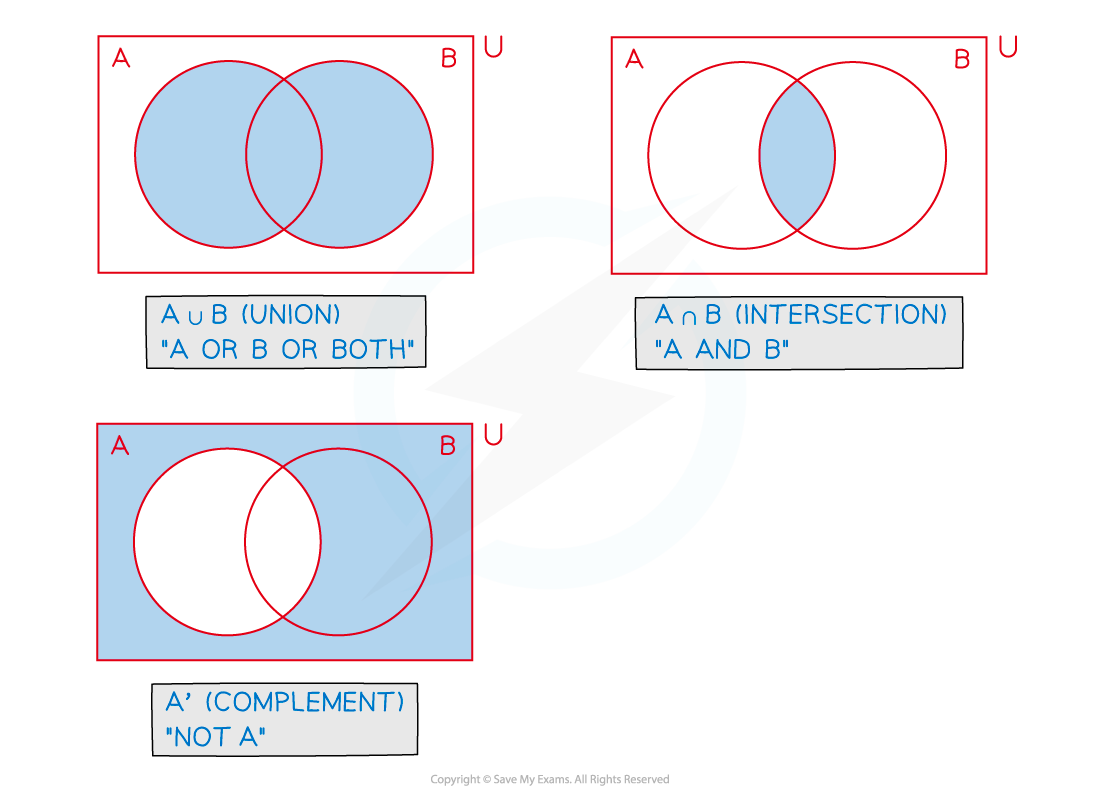
  • A Venn diagram consists of
    • a rectangle representing the sample space (U)
      • The rectangle is labelled U 
      • Some mathematicians instead use S or ξ 
    • a circle for each event
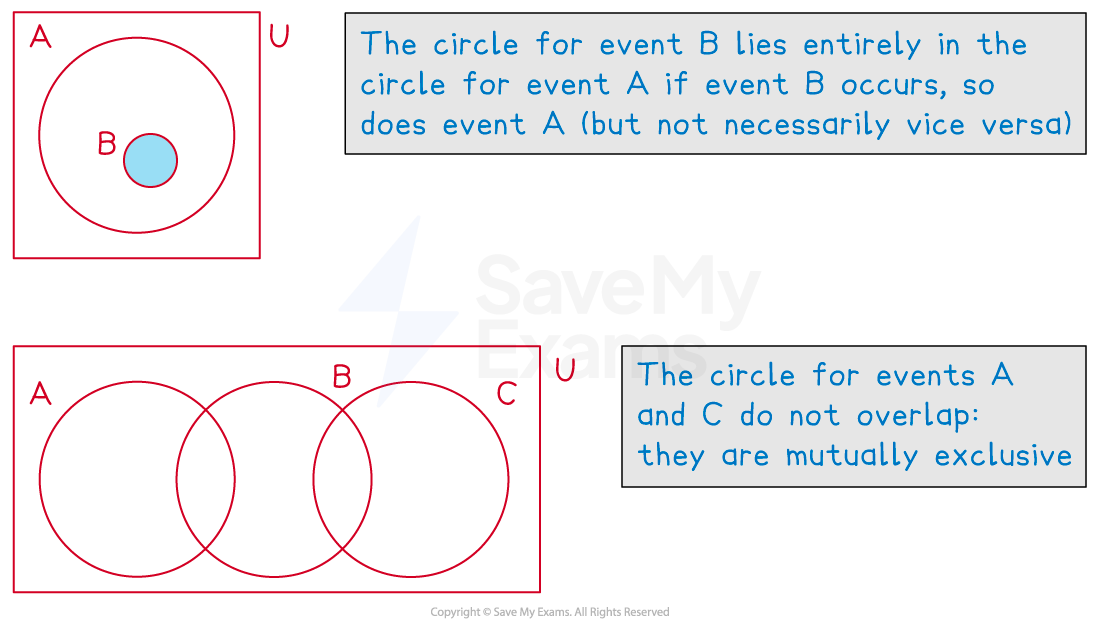
      • Circles may or may not overlap depending on which outcomes are shared between events
  • The numbers in the circles represent either the frequency of that event or the probability of that event
    • If the frequencies are used then they should add up to the total frequency
    • If the probabilities are used then they should add up to 1

What do the different regions mean on a Venn diagram? 

  • A apostrophe is represented by the regions that are not in the A circle
  • A intersection B is represented by the region where the A and B circles overlap
  • A union B is represented by the regions that are in A or B or both
  • Venn diagrams show ‘AND’ and ‘OR’ statements easily
  • Venn diagrams also instantly show mutually exclusive events as these circles will not overlap
  • Independent events can not be instantly seen
    • You need to use probabilities to deduce if two events are independent

3-2-1-fig1-venn-and-set-notation

3-1-2-fig2-various-venns-part-2

How do I solve probability problems involving Venn diagrams?

  • Draw, or add to a given Venn diagram, filling in as many values as possible from the information provided in the question
  • It is usually helpful to work from the centre outwards
    • Fill in intersections (overlaps) first
  • If two events are independent you can use the formula
    • straight P left parenthesis A intersection B right parenthesis equals straight P left parenthesis A right parenthesis straight P left parenthesis B right parenthesis
  • To find the conditional probability straight P left parenthesis A vertical line B right parenthesis
    • Add together the frequencies/probabilities in the B circle
      • This is your denominator
    • Out of those frequencies/probabilities add together the ones that are also in the A circle
      • This is your numerator
    • Evaluate the fraction

plx9zFR~_3-2-2-fig1-set-notation-examples

Examiner Tip

  • If you struggle to fill in a Venn diagram in an exam:
    • Label the missing parts using algebra
    • Form equations using known facts such as:
      • the sum of the probabilities should be 1
      • P(A∩B)=P(A)P(B) if A and B are independent events

Worked example

40 people are asked if they have sugar and/or milk in their coffee. 21 people have sugar, 25 people have milk and 7 people have neither.

a)
Draw a Venn diagram to represent the information.

4-3-3-ib-ai-aa-sl-venn-diagram-a-we-solution

b)
One of the 40 people are randomly selected, find the probability that they have sugar but not milk with their coffee.

4-3-3-ib-ai-aa-sl-venn-diagram-b-we-solution

c)
Given that a person who has sugar is selected at random, find the probability that they have milk with their coffee.

4-3-3-ib-ai-aa-sl-venn-diagram-c-we-solution

Did this video help you?

Tree Diagrams

What is a tree diagram?

  • A tree diagram is another way to show the outcomes of combined events
    • They are very useful for intersections of events
  • The events on the branches must be mutually exclusive
    • Usually they are an event and its complement
  • The probabilities on the second sets of branches can depend on the outcome of the first event
    • These are conditional probabilities
  • When selecting the items from a bag:
    • The second set of branches will be the same as the first if the items are replaced
    • The second set of branches will be the different to the first if the items are not replaced

How are probabilities calculated using a tree diagram?

  • To find the probability that two events happen together you multiply the corresponding probabilities on their branches
    • It is helpful to find the probability of all combined outcomes once you have drawn the tree
  • To find the probability of an event you can:
    • add together the probabilities of the combined outcomes that are part of that event
      • For example: straight P left parenthesis A union B right parenthesis equals straight P left parenthesis A intersection B right parenthesis plus straight P left parenthesis A intersection B apostrophe right parenthesis plus straight P left parenthesis A apostrophe intersection B right parenthesis
    • subtract the probabilities of the combined outcomes that are not part of that event from 1
      • For example: straight P left parenthesis A union B right parenthesis equals 1 minus straight P left parenthesis A apostrophe intersection B apostrophe right parenthesis

UclzomJM_3-2-3-fig1-tree-setup

Do I have to use a tree diagram?

  • If there are multiple events or trials then a tree diagram can get big
  • You can break down the problem by using the words AND/OR/NOT to help you find probabilities without a tree
  • You can speed up the process by only drawing parts of the tree that you are interested in

Which events do I put on the first branch?

  • If the events A and B are independent then the order does not matter
  • If the events A and B are not independent then the order does matter
    • If you have the probability of A given B then put B on the first set of branches
    • If you have the probability of B given A then put A on the first set of branches

Examiner Tip

  • In an exam do not waste time drawing a full tree diagram for scenarios with lots of events unless the question asks you to
    • Only draw the parts that you are interested in

Worked example

20% of people in a company wear glasses. 40% of people in the company who wear glasses are right-handed. 50% of people in the company who don’t wear glasses are right-handed.

a)
Draw a tree diagram to represent the information.

4-3-3-ib-ai-aa-sl-tree-diagram-a-we-solution

b)
One of the people in the company are randomly selected, find the probability that they are right-handed.

4-3-3-ib-ai-aa-sl-tree-diagram-b-we-solution

c)
Given that a person who is right-handed is selected at random, find the probability that they wear glasses.

4-3-3-ib-ai-aa-sl-tree-diagram-c-we-solution

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcards

    Did this page help you?

    Previous:4.3.2 Conditional ProbabilityNext:4.4.1 Discrete Probability Distributions
    Dan

    Author: Dan

    Expertise: Maths

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.