Reciprocal Transformations (DP IB Analysis & Approaches (AA)): Revision Note
Reciprocal transformations
What is a reciprocal transformation?
For the graph
the reciprocal transformation is
It transforms points on the graph
by changing their
-coordinates
from a height of
to a height of
All
-coordinates stay the same
Points that lie on the line y = 1 or the line y = -1 stay the same
Examiner Tips and Tricks
It helps to know, when sketching, that any points with -coordinates of
stay the same under a reciprocal transformation.
How do I sketch a reciprocal transformation y = 1/f(x)?
To sketch a reciprocal transformation, you need to know
how key features on the original graph
transform to different key features on the graph of
In general
the larger the heights of points on
the closer to the
-axis they become on
and vice versa
If
is positive
then
is positive
If
is negative
then
is negative
If
is increasing
then
is decreasing
If
is decreasing
then
is increasing
More specifically
If
has a
-intercept at
where
has a
-intercept at
If
has an
-intercept (root)at
has a vertical asymptote at
If
has a vertical asymptote at
has a discontinuity at
The discontinuity looks like a root when you sketch
If
has a local maximum at
where
has a local minimum at
If
has a local minimum at
where
has a local maximum at
If
has a horizontal asymptote at
if
then
has a horizontal asymptote at
if
then
If
as
has a horizontal asymptote at
Worked Example
The diagram below shows the graph of which has a local maximum at the point
.
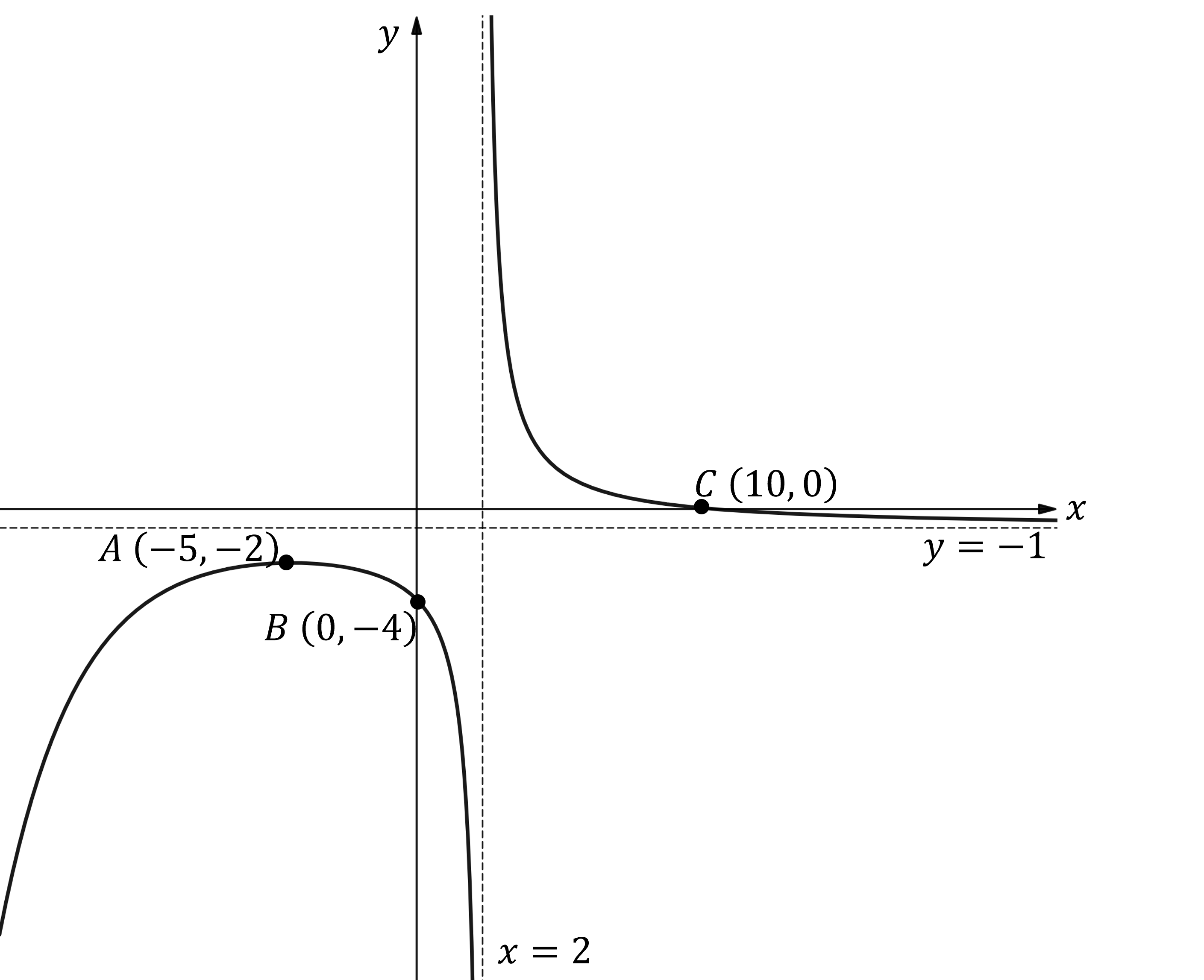
Sketch the graph of .
Answer:
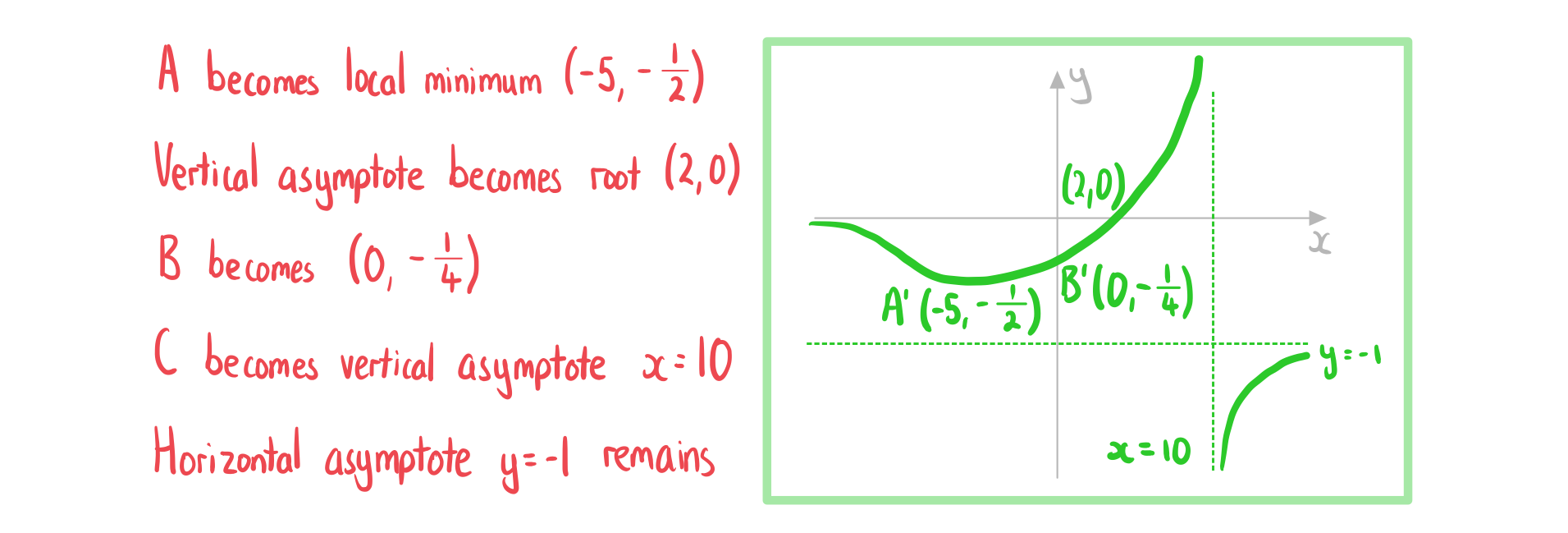

Unlock more, it's free!
Did this page help you?