Quadratic Functions (DP IB Analysis & Approaches (AA)): Revision Note
Did this video help you?
Quadratic functions & graphs
What are the key features of quadratic graphs?
A quadratic graph can be written in the form
where
The value of
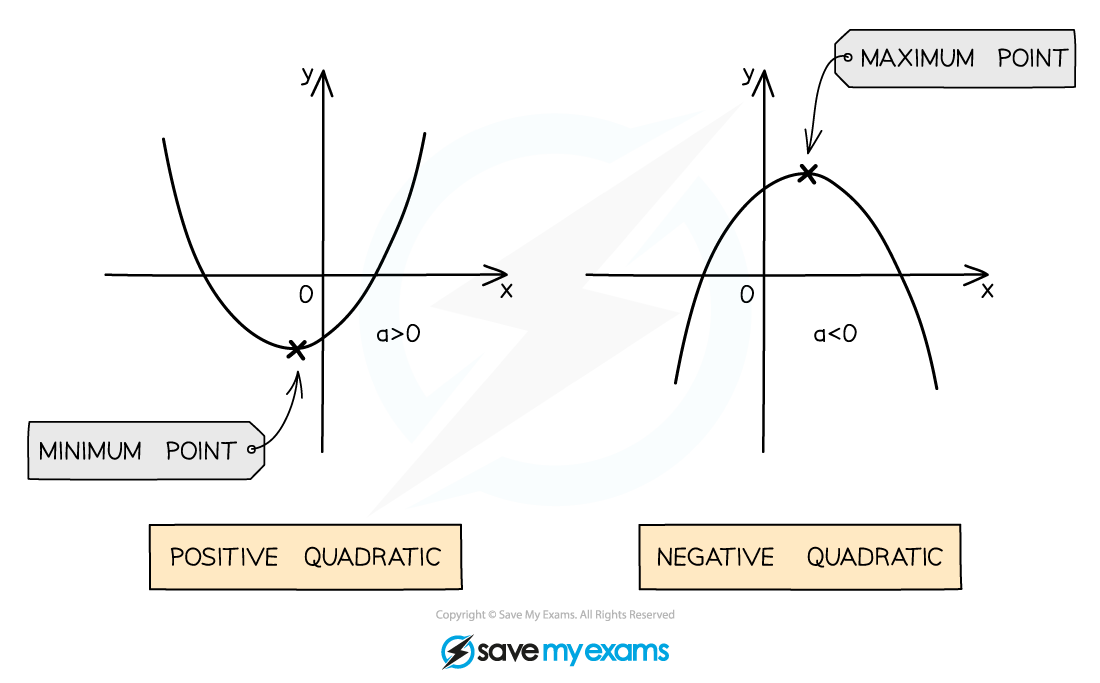
affects the shape of the curve
If
is positive the shape is concave up
The graph has a minimum point
If
is negative the shape is concave down
The graph has a maximum point
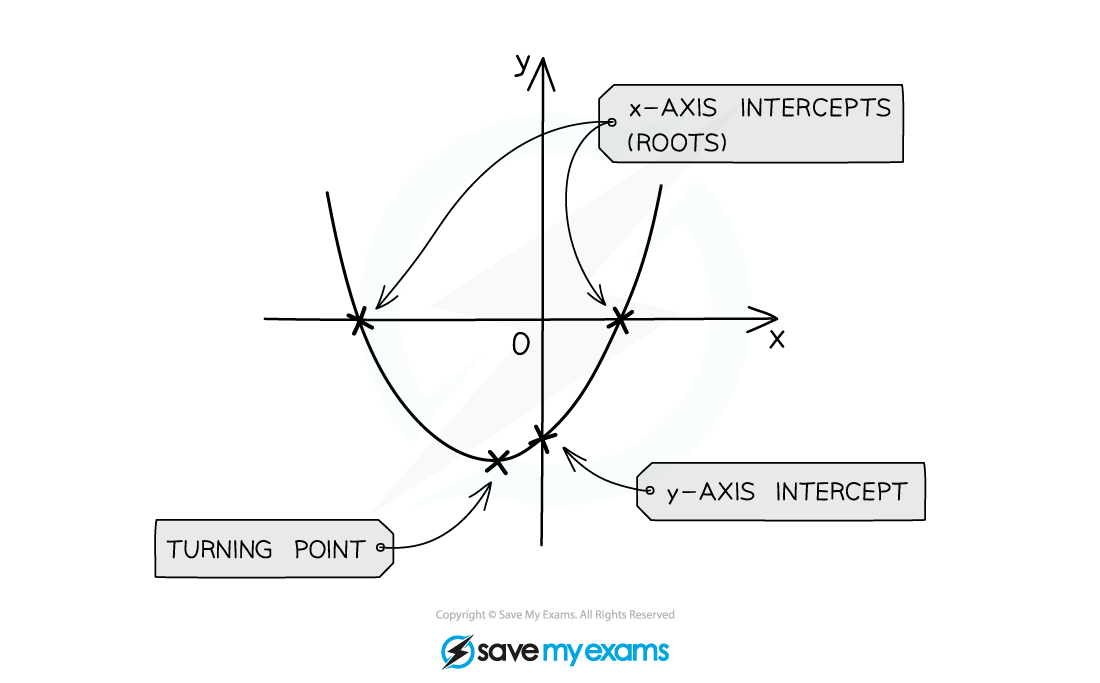
The
-intercept is at the point
The zeros or roots are the solutions to
These can be found by
Factorising
Quadratic formula
Using your GDC
These are also called the
-intercepts
A quadratic graph can have 0, 1 or 2
-intercepts
This is determined by the value of the discriminant
There is an axis of symmetry at
This is given in your formula booklet
If there are two
-intercepts then the axis of symmetry goes through their midpoint
E.g. If there are roots at
and
then the axis of symmetry is at
The vertex lies on the axis of symmetry
It can be found by completing the square
The
-coordinate of the vertex is
The
-coordinate can be found using your GDC or by calculating
when
If
is positive then the vertex is the minimum point
If
is negative then the vertex is the maximum point
What are the equations of a quadratic function?
This is the general form
It clearly shows the
-intercept
The axis of symmetry is
This is given in the formula booklet
This is the factorised form
It clearly shows the roots
and
The axis of symmetry is
This is the vertex form
It clearly shows the vertex
The axis of symmetry is therefore
It clearly shows how the function can be transformed from the graph
Vertical stretch by scale factor
Translation by vector
How do I sketch a quadratic graph?
Determine its shape by looking at the value of
e.g.
looks like
Find the axis of symmetry using the formula
e.g.
Find the vertex by substituting the x-coordinate into the equation or by completing the square
e.g.
or
vertex is at
Find the roots by setting the expression equal to zero and solving
e.g.
roots are
and
Label the y-intercept
e.g.
Draw the graph going through all the labelled points
How do I find an equation of a quadratic?
If you have the roots
and
,
Write in factorised form
You will need a third point on the curve to substitute in to find the value of
If you have the vertex
,
Write in vertex form
You will need a second point on the curve to find the value of
If you have three random points
,
and
,
Write in the general form
Substitute the three points into the equation, one at a time
Form and solve a system of three linear equations to find the values of
,
and
Examiner Tips and Tricks
Use your GDC to find the roots and the turning point of a quadratic function. You do not need to factorise or complete the square.
It is good exam technique to sketch the graph from your GDC as part of your working.
Worked Example
The diagram below shows the graph of , where
is a quadratic function.
The intercept with the -axis and the vertex have been labelled.
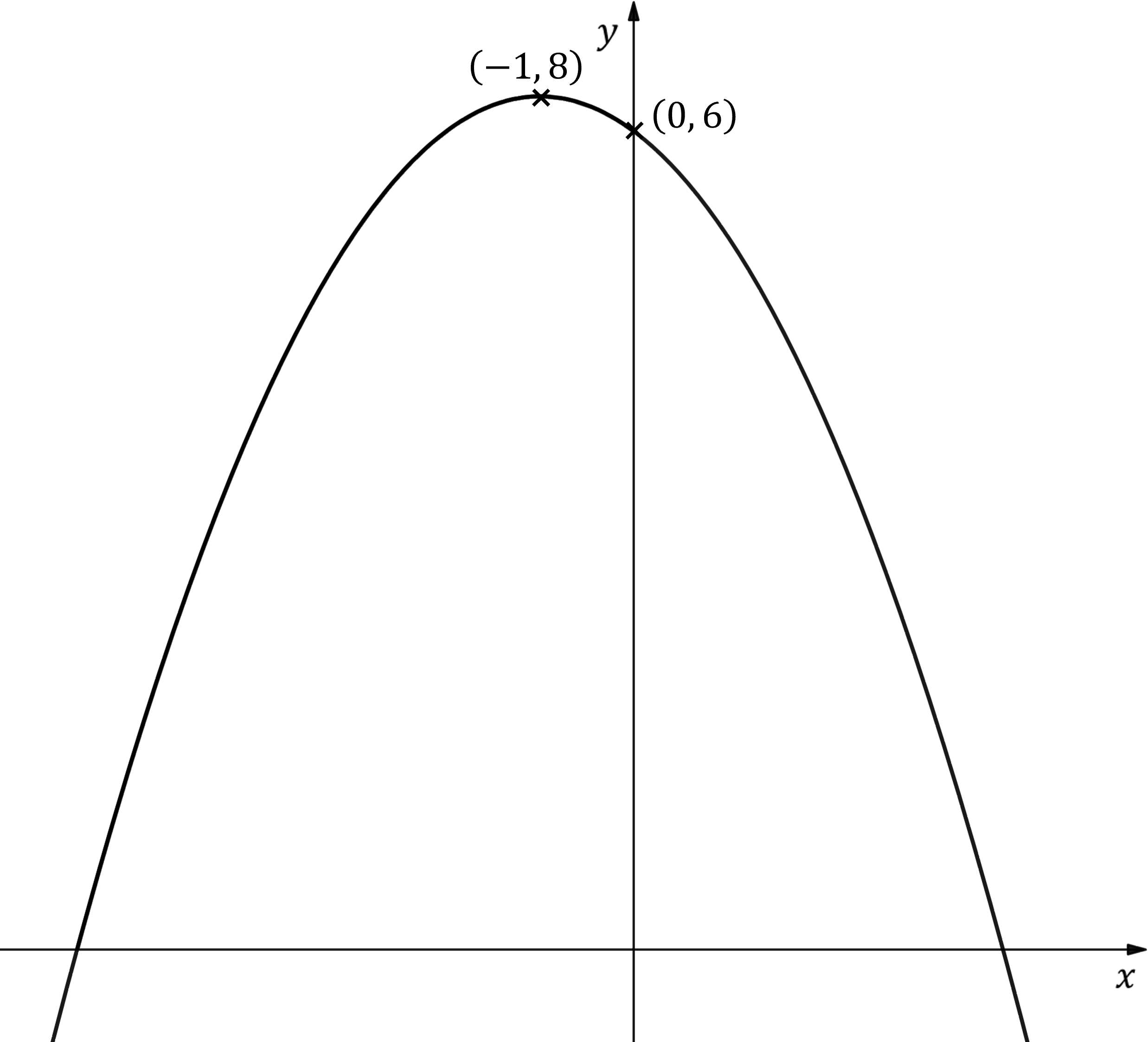
Write down an expression for .
Answer:


Unlock more, it's free!
Did this page help you?