Probability Density Function (DP IB Analysis & Approaches (AA)): Revision Note
Did this video help you?
Calculating probabilities using PDF
A continuous random variable can take any value in an interval so is typically used when continuous quantities are involved (time, distance, weight, etc)
What is a probability density function (p.d.f.)?
For a continuous random variable, a function can be used to model probabilities
This function is called a probability density function (p.d.f.), denoted by f(x)
For f(x) to represent a p.d.f. the following conditions must apply:
f(x) ≥ 0 for all values of x
The area under the graph of y = f(x) must total 1
In most problems, the domain of f(x) is restricted to an interval, a ≤ x ≤ b say, with all values of x outside of the interval having f(x)=0
How do I find probabilities using a probability density function (p.d.f.)?
The probability that the continuous random variable X lies in the interval a ≤ X ≤ b, where X has the probability density function f(x), is given by
For any continuous random variable (including the normal distribution), the following are true:
I.e.
and
are interchangeable
, for any single value
Because
For linear functions it can be easier to calculate the probability integral using areas of geometric shapes
Rectangle: A = bh
Triangle: A = ½(bh)
Trapezoid: A = ½(a+b)h
How do I determine whether a function is a valid pdf?
Some questions may ask you to justify the use of a given function as a probability density function
In such cases check and confirm that the function meets the two conditions
f(x) ≥ 0 for all values of x
total area under the graph is 1
Examiner Tips and Tricks
Don't forget the condition. A common error is to confirm that the total area is equal to 1, but to forget to confirm that
is always true.
How do I use a pdf to find probabilities?
STEP 1
Identify the probability density function, f(x) - this may be given as a graph, an equation or as a piecewise functione.g.
Identify the limits of x for a particular problem
Remember that P(a ≤ X ≤ b) = P(a < X < b)
STEP 2
Sketch, or use your GDC to draw, the graph of y = f(x)Look for basic shapes (rectangles, triangles and trapezoids) as finding these areas is easier without using integration
Look for symmetry in the graph that may make the problem easier
Break the area required into two or more parts if it makes the problem easier
STEP 3
Find the area(s) required using basic shapes or integration and answer the question
Trickier problems may ask you to find one of the integration limits of the integral given the value of a probability
e.g. Find the value of
given that
Worked Example
The continuous random variable, X, has probability density function
a) Show that f(x) is a valid probability density function.
Answer:

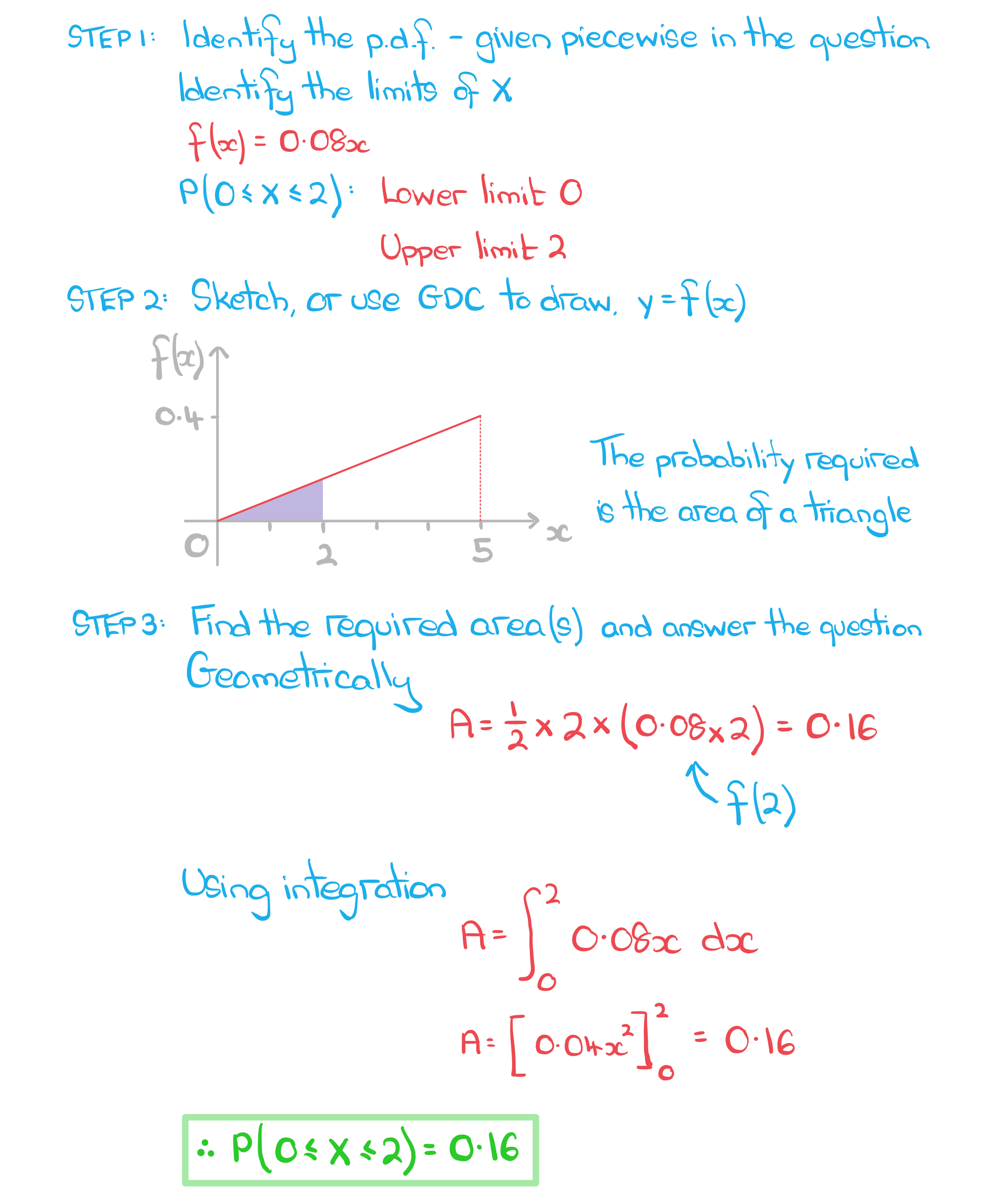
b) Find, both geometrically and using integration, P(0 ≤ X ≤ 2).
Answer:
c) Write down P(X = 3.2).
Answer:
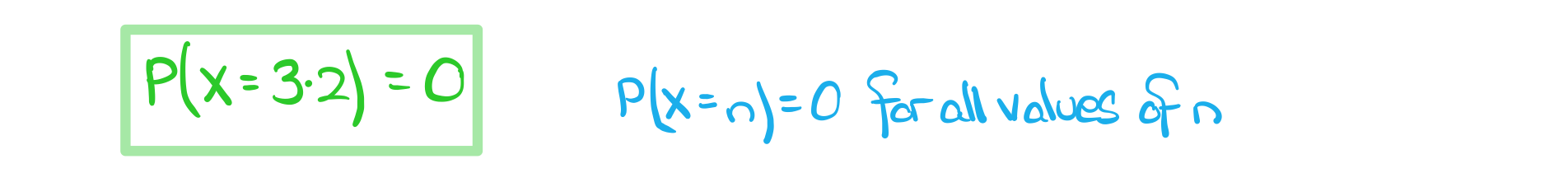

Unlock more, it's free!
Did this page help you?