Introduction to Derivatives (DP IB Analysis & Approaches (AA)): Revision Note

Introduction to Derivatives

• Before introducing a derivative, an understanding of a limit is helpful

What is a limit?

• The limit of a function is the value a function (of ) approaches as  approaches a particular value from either side

  • Limits are of interest when the function is undefined at a particular value

  • For example, the function will approach a limit as approaches 1 from both below and above but is undefined at  as this would involve dividing by zero

What might I be asked about limits?

• You may be asked to predict or estimate limits from a table of function values or from the graph of 

• You may be asked to use your GDC to plot the graph and use values from it to estimate a limit

What is a derivative?

• Calculus is about rates of change

  • the way a car’s position on a road changes is its speed (velocity)

  • the way the car’s speed changes is its acceleration

• The gradient (rate of change) of a (non-linear) function varies with 

• The derivative of a function is a function that relates the gradient to the value of 

• The derivative is also called the gradient function

How are limits and derivatives linked?

• Consider the point  on the graph of  as shown below

  •  is a series of chords

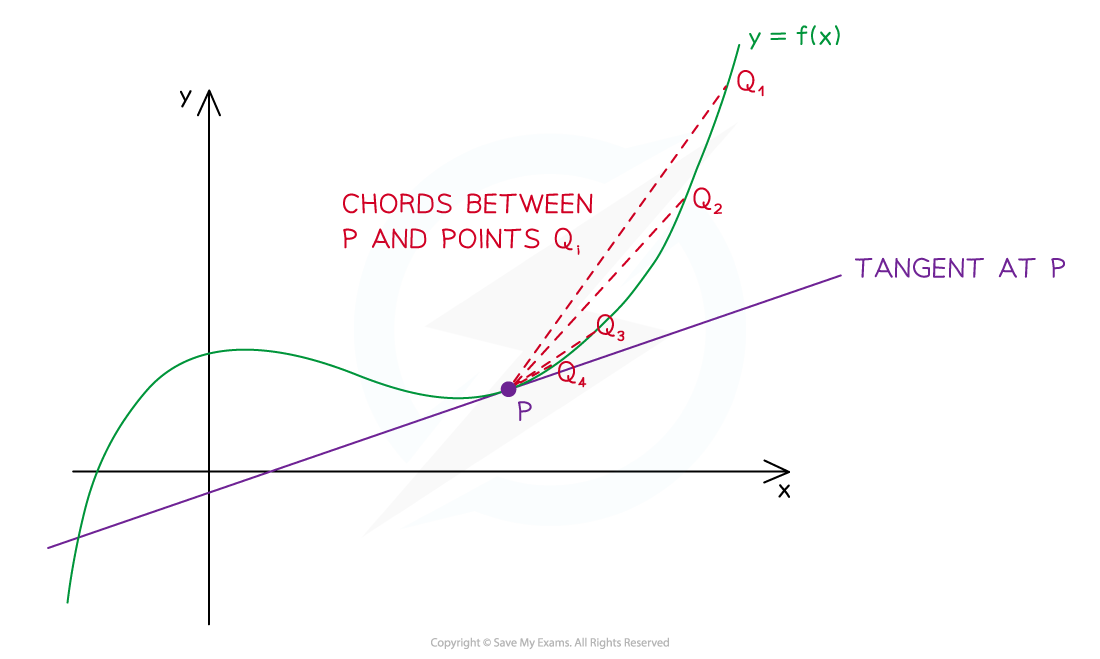
• The gradient of the function at the point  is equal to the gradient of the tangent at point 

• The gradient of the tangent at point  is the limit of the gradient of the chords  as point  ‘slides’ down the curve and gets ever closer to point 

• The gradient of the function changes as  changes

• The derivative is the function that calculates the gradient from the value 

What is the notation for derivatives?

• For the function , the derivative, with respect to , would be written as

• Different variables may be used

  • e.g. If  then