Translations of Graphs (DP IB Analysis & Approaches (AA)): Revision Note
Did this video help you?
Translations of graphs
What are translations of graphs?
A translation is when:
the graph is moved (up or down, left or right) in the
plane
i.e. its position changes
but the shape, size, and orientation remain unchanged
How far left/right or up/down is specified by a translation vector
:
is the horizontal displacement
Positive moves right
Negative moves left
is the vertical displacement
Positive moves up
Negative moves down

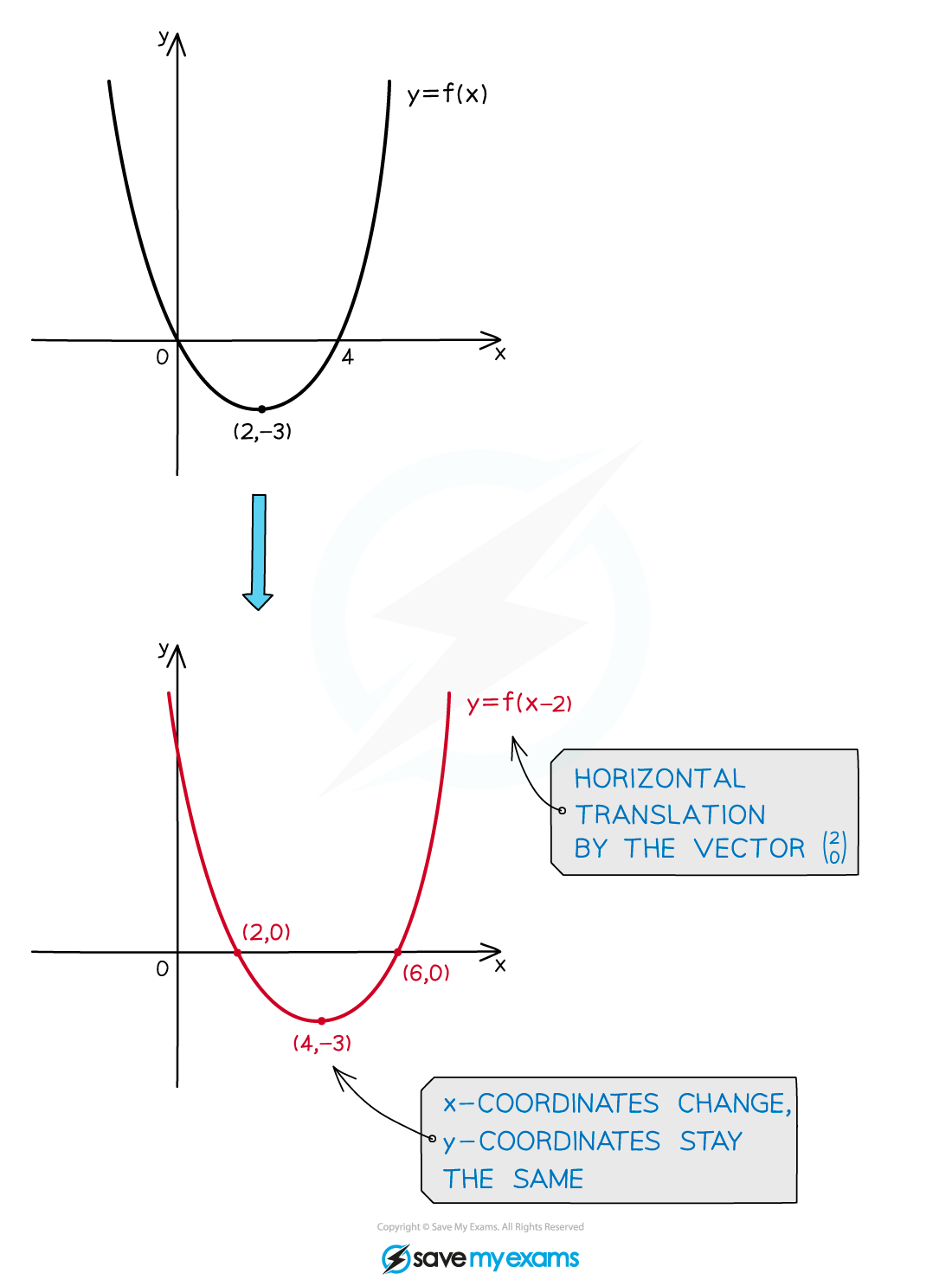
How do I find the graph equation after a horizontal translation?
A horizontal translation of the graph
by
units to the right, i.e. the vector
, is represented by the equation
Examiner Tips and Tricks
It is a common mistake to think that is replaced by
when translating
units to the right!
Any vertical asymptotes will also be translated
becomes
Horizontal asymptotes stay the same
To translate a graph
units to the left
i.e. the vector
the equation becomes
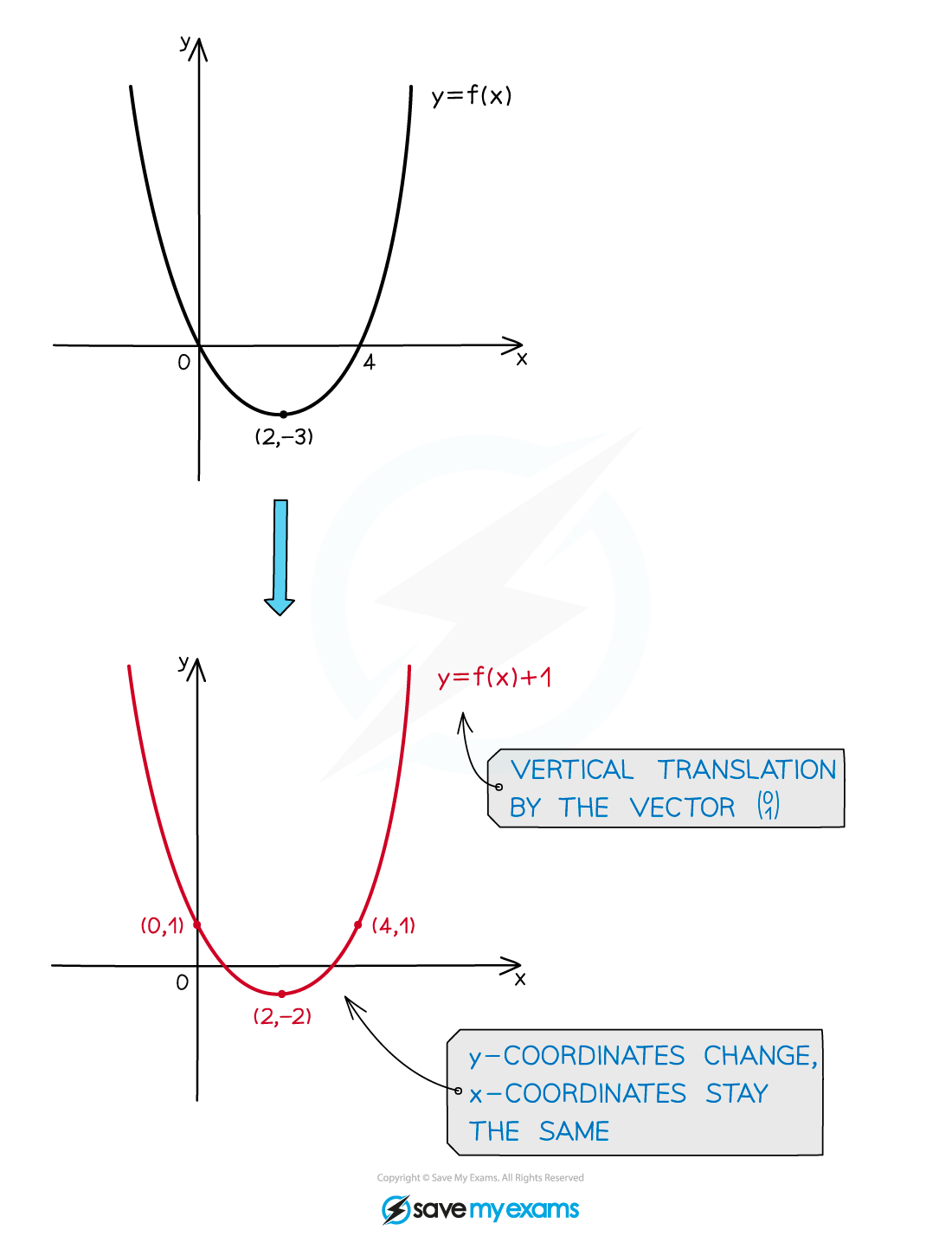
How do I find the graph equation after a vertical translation?
A vertical translation of the graph
by
units up, i.e. the vector
, is represented by
Similarly a vertical translation
units down
i.e. the vector
has the equation
Horizontal asymptotes change
becomes
Vertical asymptotes stay the same
Examiner Tips and Tricks
To get full marks in an exam make sure you use correct mathematical terminology, e.g. translate by the vector .
Worked Example
The diagram below shows the graph of .
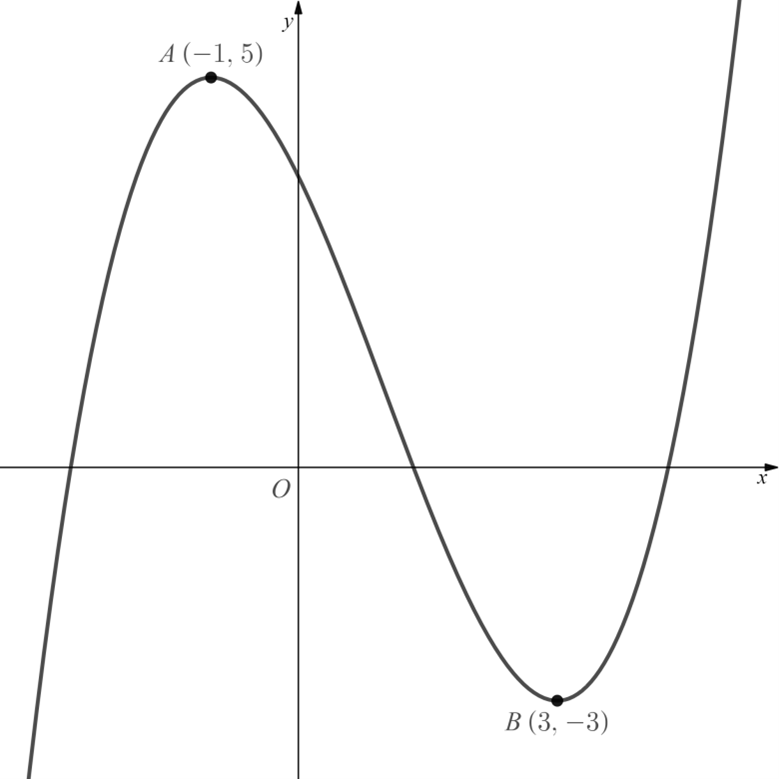
(a) Sketch the graph of .
Answer:

(b) Sketch the graph of .
Answer:


Unlock more, it's free!
Did this page help you?