Displacement, Velocity & Acceleration (DP IB Analysis & Approaches (AA)): Revision Note

Displacement, velocity & acceleration

What is kinematics?

• Kinematics is the branch of mathematics that models and analyses the motion of objects

• Common words such as distance, speed and acceleration are used in kinematics but are used according to their technical definition

What definitions do I need to be aware of?

• In this course, only motion of an object in a straight line is considered

  • This could be a horizontal straight line

    • The positive direction will usually be to the right

  • Or this could be a vertical straight line

    • The positive direction will usually be upwards

Particle

• A particle is the general term for an object

  • Some questions may use a specific object such as a car or a ball

Time  seconds

• Displacement, velocity and acceleration are all functions of time

• Initially time is zero, 

Displacement  m

• The displacement of a particle is its distance relative to a fixed point

  • The fixed point is often (but not always) the particle’s initial position

• Displacement will be zero, , if the object is at or has returned to its initial position

• Displacement will be negative if its position relative to the fixed point is in the negative direction (left or down)

Distance  m

• Use of the word distance needs to be considered carefully and could refer to

  • the distance travelled by a particle

  • the (straight line) distance the particle is from a particular point

• Be careful not to confuse displacement with distance

  • If a bus route starts and ends at a bus depot, then when the bus has returned to the depot

    • its displacement will be zero 

    • but the distance the bus has travelled will be the length of the route

• Distance is always positive

Velocity m s^-1

• The velocity of a particle is the rate of change of its displacement at time

• Velocity will be negative if the particle is moving in the negative direction

• A velocity of zero means the particle is stationary, 

Speed  m s^-1

• Speed is the magnitude (a.k.a. absolute value or modulus) of velocity

  • For a particle moving in a straight line, speed is the velocity ignoring the direction

    • if

    • if

Acceleration  m s^-2

• The acceleration of a particle is the rate of change of its velocity at time

• Acceleration can be negative but this alone cannot fully describe the particle’s motion

  • if velocity and acceleration have the same sign the particle is accelerating (speeding up)

  • if velocity and acceleration have different signs then the particle is decelerating (slowing down)

  • if acceleration is zero the particle is moving with constant velocity 

  • in all cases the direction of motion is determined by the sign of velocity

Are there any other words or phrases in kinematics I should know?

• Certain words and phrases can imply values or directions in kinematics

  • a particle described as “at rest” means that its velocity is zero,

  • a particle described as moving “due east” or “right” or would be moving in the positive horizontal direction

    • this also means that

  • a particle “dropped from the top of a cliff” or moving “down” would be moving in the negative vertical direction

    • this also means that

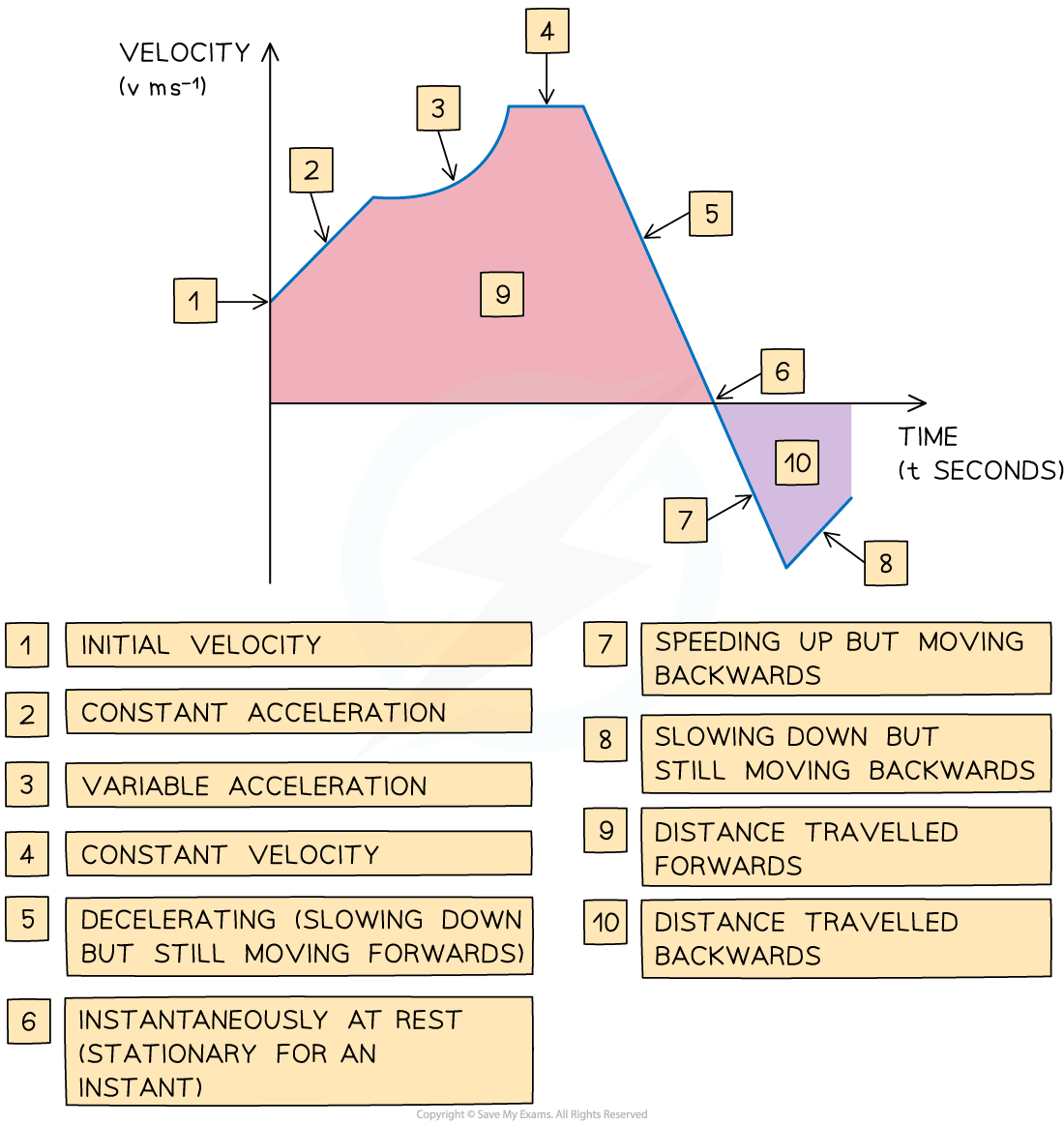
What are the key features of a velocity-time graph?

• The gradient of the graph equals the acceleration  of an object

• A straight line shows that the object is accelerating at a constant rate

• A horizontal line shows that the object is moving at a constant velocity

• The area between the graph and the x-axis tells us the change in displacement of the object

  • Graph above the x-axis means the object is moving forwards

  • Graph below the x-axis means the object is moving backwards

• The total displacement of the object from its starting point is the sum of the areas above the x-axis minus the sum of the areas below the x-axis

• The total distance travelled by the object is the sum of all the areas

• If the graph touches the x-axis then the object is stationary at that time

• If the graph is above the x-axis then the object has positive velocity and is travelling forwards

• If the graph is below the x-axis then the object has negative velocity and is travelling backwards