Graphical Representation of Gravitational Potential (AQA A Level Physics): Revision Note

Graphical Representation of Gravitational Potential

• Gravitational field strength, g and the gravitational potential, V can be graphically represented against the distance from the centre of a planet, r

• g, V and r are related by the equation:

• Where:

  • g = gravitational field strength (N kg^-1)

  • ΔV = change in gravitational potential (J kg^-1)

  • Δr = distance from the centre of a point mass (m)

• The graph of V against r for a planet is:

The gravitational potential and distance graphs follows a -1/r relation

• The key features of this graph are:

  • The values for V are all negative  (because the graph is drawn below the horizontal r axis)

  • As r increases, V against r follows a -1/r relation

  • The graph has a shallow increase as r increases

• To calculate the magnitude of g, draw a tangent to the graph at that point and calculate the gradient of the tangent to find

• The gravitational field strength is the negative of this gradient,

  • The minus sign shows the field points towards the planet (i.e. towards lower potential)

• This is a graphical representation of the equation:

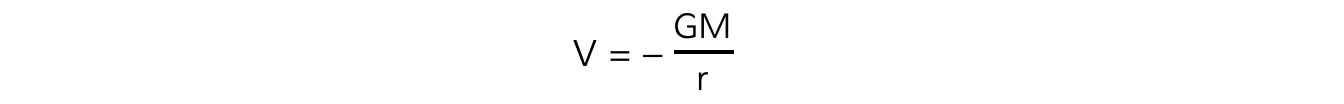
where G and M are constant

• The graph of g against r for a planet is:

The gravitational field strength and distance graph follows a 1/r2 relation

• The key features of this graph are:

  • The values for g are all positive

  • As r increases, g against r follows a 1/r² relation (inverse square law)

  • The magnitude of the area under this graph is the magnitude of the change in gravitational potential ΔV

    • i.e. the area represents the change in gravitational potential

  • The graph has a steep decline as r increases

• The area under the graph can be estimated by counting squares, if it is plotted on squared paper, or by splitting it into trapeziums and summing the area of each trapezium

• The inverse square law relation means that as the distance r doubles, g decreases by a factor of 4

• This is a graphical representation of the equation:

where G and M are constant