A LevelPhysicsAQARevision NotesNuclear PhysicsNuclear Fusion & FissionNuclear Fusion & Fission

Nuclear Fusion & Fission (AQA A Level Physics): Revision Note

Exam code: 7408

Katie M

Author

Katie M

Last updated

Nuclear Fusion & Fission

Nuclear fusion

  • Nuclear fusion is defined as:

The joining together of two small nuclei to produce a larger nucleus

  • Low mass nuclei, such as hydrogen and helium, can undergo fusion and release energy

  • For example, when two hydrogen nuclei (protons) fuse, a deuterium nucleus is produced

    • A positron and an electron neutrino are also produced as one of the protons converts into a neutron through beta-plus decay

straight H presubscript 1 presuperscript 1 space plus thin space straight H presubscript 1 presuperscript 1 space rightwards arrow space straight H presubscript 1 presuperscript 2 space plus thin space straight e to the power of plus space plus thin space straight nu subscript straight e

  • In the centres of stars, four hydrogen nuclei open parentheses straight H presubscript 1 presuperscript 1 close parentheses fuse to produce a helium nucleus open parentheses He presubscript 2 presuperscript 4 close parentheses, plus the release of energy

    • This provides fuel for the star to continue burning

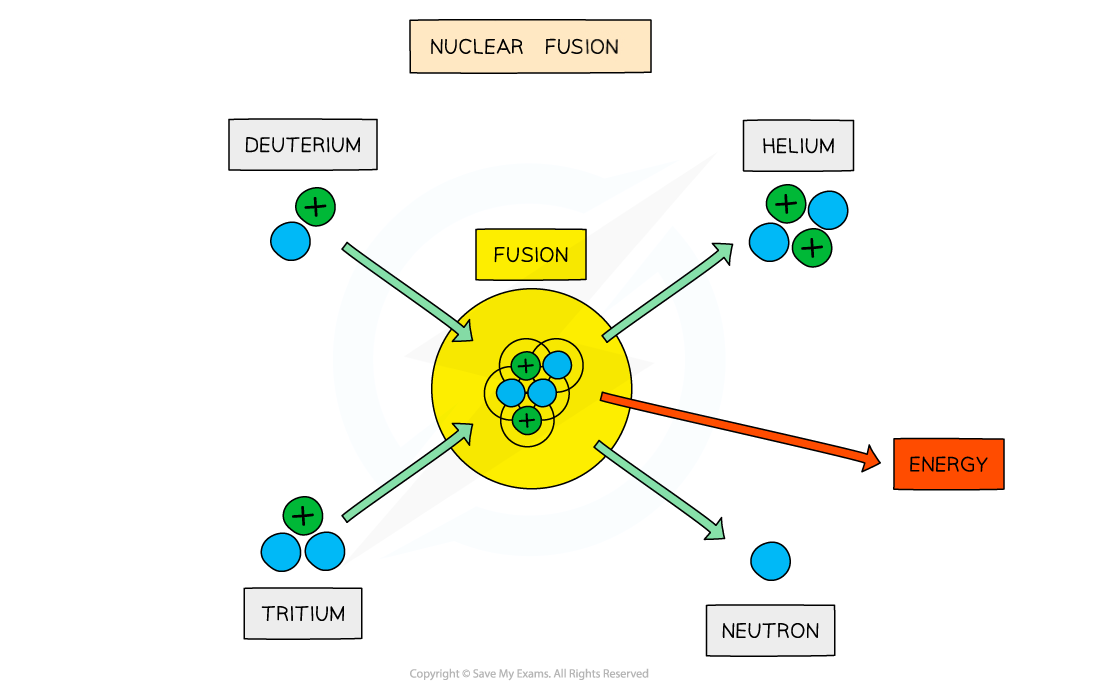
  • On Earth, research is focused on achieving the deuterium-tritium (D-T) reaction

  • This involves fusing a deuterium nucleus and a tritium nucleus together to produce a helium nucleus and a neutron

straight H presubscript 1 presuperscript 2 space plus thin space straight H presubscript 1 presuperscript 3 space rightwards arrow space He presubscript 2 presuperscript 4 space plus thin space straight n presubscript 0 presuperscript 1

Deuterium-tritium fusion

A nuclear fusion reaction, where deuterium and tritium combine to form helium, releasing a neutron and energy.
The fusion of deuterium and tritium nuclei to form a helium nucleus and a neutron, with the release of energy

  • For two nuclei to fuse, both nuclei must have high kinetic energy

  • This is because nuclei must be able to get close enough to fuse

  • However, two forces acting within the nuclei make this difficult to achieve

    • Electrostatic repulsion 

      • Protons inside the nuclei are positively charged, which means that they electrostatically repel one another

    • Strong nuclear force

      • The strong nuclear force, which binds nucleons together, acts at very short distances within nuclei

      • Therefore, nuclei must get very close together for the strong nuclear force to take effect

  • It takes a great deal of energy to overcome the electrostatic force, hence, fusion can only be achieved in an extremely hot, dense environment, such as the core of a star

Nuclear fission

  • Nuclear fission is defined as:

The splitting of a large atomic nucleus into smaller nuclei

  • High mass nuclei (such as uranium) can undergo fission and release energy

Induced fission

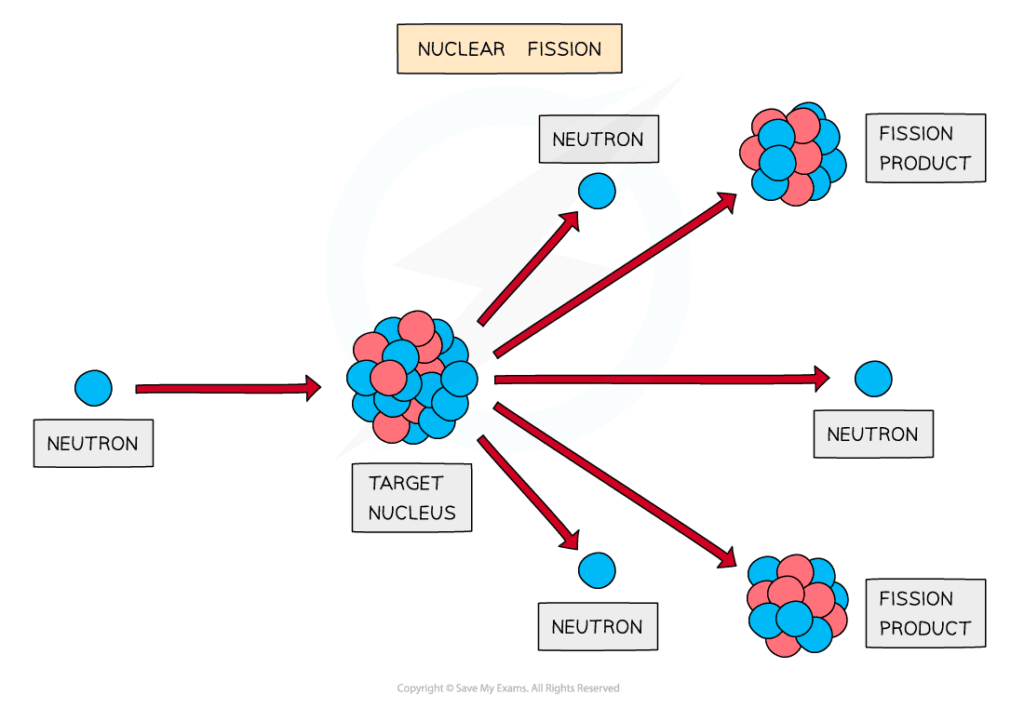
The process of nuclear fission, where a neutron hits a target nucleus, causing it to split into two fission products and three neutrons.
The fission of a target nucleus, such as uranium, to produce smaller daughter nuclei, with the release of energy

  • Fission must be induced by firing neutrons at a nucleus

    • When a neutron strikes a nucleus, it splits into two or more daughter nuclei

    • During fission, neutrons are ejected from the nucleus, which in turn can collide with other nuclei, triggering a cascade effect

    • This leads to a chain reaction, which lasts until all of the material has undergone fission, or the reaction is halted by a moderator

  • Nuclear fission is the process which produces energy in nuclear power stations, where it is well controlled

  • When nuclear fission is not controlled, the chain reaction can cascade to produce the effects of a nuclear bomb

Examiner Tips and Tricks

When an atom undergoes nuclear fission, take note that extra neutrons are ejected by the nucleus and not from the fission products

Calculating Energy Released in Nuclear Reactions

  • The binding energy is equal to the amount of energy released in forming the nucleus, and can be calculated using:

E space equals space increment m c squared

  • Where:

    • E = Binding energy released (J)

    • Δm = mass defect (kg)

    • c = speed of light (m s-1)

  • The daughter nuclei produced as a result of both fission and fusion have a higher binding energy per nucleon than the parent nuclei

  • Therefore, energy is released as a result of the mass difference between the parent nuclei and the daughter nuclei

Worked Example

When a uranium-235 nucleus absorbs a slow-moving neutron and undergoes fission one possible pair of fission fragments is technetium-112 and indium-122. The equation for this process and the binding energy per nucleon for each isotope is shown below.

Binding energy per nucleon of U-235 = 7.59 MeV

Binding energy per nucleon of Tc-112 = 8.36 MeV

Binding energy per nucleon of In-122 = 8.51 MeV

When a uranium-235 nucleus undergoes fission in this way, calculate:

(a) The energy released, in MeV

(b) The mass defect

Answer:

Part (a)

Step 1: Determine the binding energies on each side of the equation

Binding energy = Binding Energy per Nucleon × Mass Number

  • Binding energy before (U) = 235 × 7.59 = 1784 MeV

  • Binding energy after (Tc + In) = (112 × 8.36) + (122 × 8.51) = 1975 MeV

Step 2: Find the difference between the energies

  • Energy released = 1975 – 1784 = 191 MeV

Part (b)

Method 1

Step 1: Convert the energy released from MeV to J

  • 1 MeV = 1.60 × 10−13 J

  • Energy released = 191 × (1.60 × 10−13) = 3.06 × 10−11 J

Step 2: Write down the equation for mass-energy equivalence

E = Δmc2

  • Where c = speed of light

Step 3: Rearrange and determine the mass defect, Δm

Δm = 3.4 × 10−28 kg

Method 2

Step 1: Convert the energy released from MeV to u

Step 2: Calculate the mass defect, Δm

  • 1 u = 1.66 × 10−27 kg

Δm = 0.205 × (1.66 × 10−27) = 3.4 × 10−28 kg

Examiner Tips and Tricks

Both methods for calculating mass defect are perfectly valid. It is highly recommended that you practice both ways and see which method you are most comfortable using.

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself
    Previous:Mass Difference & Binding EnergyNext:Binding Energy
    Katie M

    Author: Katie M

    Expertise: Physics Content Creator

    Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.